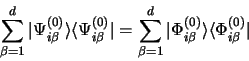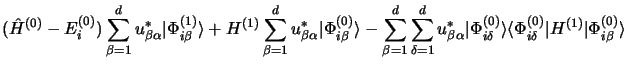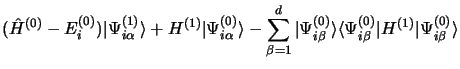suivant: Exemple : l'effet Stark
monter: Perturbations statiques.
précédent: États non dégénérés
Pour un état 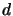 fois dégénéré, les dénominateurs des équations
3.57 et 3.58 peuvent être nuls sans que les
numérateurs le
soient. Dans ce cas la correction de la fonction d'onde au premier ordre ainsi
que la correction du deuxième ordre à l'énergie divergent, et ne sont donc
pas physiques. Deux méthodes peuvent être utilisées pour traiter le cas
des niveaux dégénérés.
fois dégénéré, les dénominateurs des équations
3.57 et 3.58 peuvent être nuls sans que les
numérateurs le
soient. Dans ce cas la correction de la fonction d'onde au premier ordre ainsi
que la correction du deuxième ordre à l'énergie divergent, et ne sont donc
pas physiques. Deux méthodes peuvent être utilisées pour traiter le cas
des niveaux dégénérés.
Dans la première méthode, on recherche une transformation unitaire 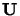 des fonctions
des fonctions
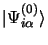 , avec
, avec
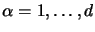
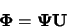 |
(3.59) |
telle que la matrice
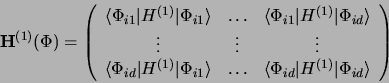 |
(3.60) |
soit diagonale. U est la matrice des vecteurs propres de la matrice
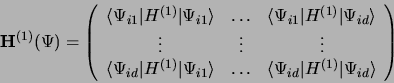 |
(3.61) |
En utilisant les fonctions
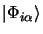 on obtient
on obtient
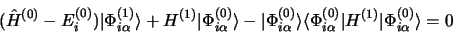 |
(3.62) |
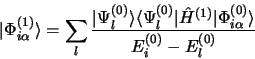 |
(3.63) |
et
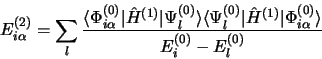 |
(3.64) |
Les termes correspondant à
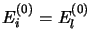 sont exclus des sommes.
sont exclus des sommes.
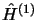 est diagonal sur la base des
est diagonal sur la base des
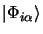 , donc
, donc
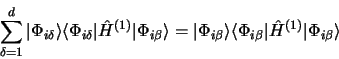 |
(3.65) |
En substituant dans l'équation 3.62, en multipliant par les
coefficients
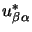 , en sommant sur l'indice
, en sommant sur l'indice 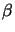 et en
utilisant l'égalité des projecteurs
et en
utilisant l'égalité des projecteurs
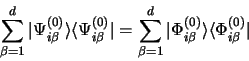 |
(3.66) |
il vient



suivant: Exemple : l'effet Stark
monter: Perturbations statiques.
précédent: États non dégénérés
Bernard Silvi
2005-03-16
![]() des fonctions
des fonctions
![]() , avec
, avec
![]()
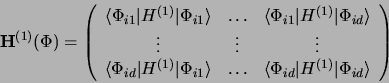
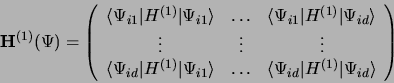
![]() est diagonal sur la base des
est diagonal sur la base des
![]() , donc
, donc