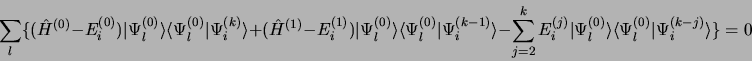suivant: États dégénérés
monter: Perturbations statiques.
précédent: Perturbations statiques.
États non dégénérés
Pour résoudre l'équation de Schrödinger dans le cas d'un état non
dégénéré
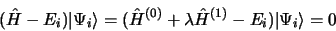 |
(3.44) |
on développe 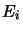 et
et
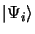 en série de
en série de 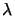
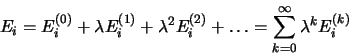 |
(3.45) |
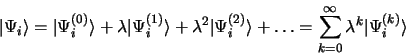 |
(3.46) |
en substituant dans l'équation 3.44, on obtient
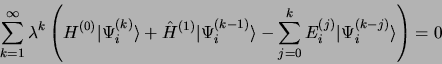 |
(3.47) |
pour que cette équation soit vérifiée indépendamment de la valeur de
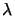 , il faut que tous les coefficients de
, il faut que tous les coefficients de 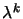 soit nuls, ce qui
engendre la suite d'équations
soit nuls, ce qui
engendre la suite d'équations
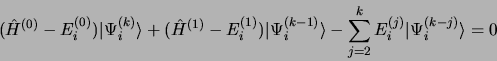 |
(3.48) |
La normalisation de
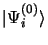 et de
et de
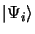 implique
3.2
implique
3.2
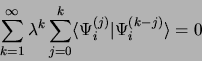 |
(3.49) |
en multipliant à gauche l'équation 3.48
par
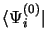
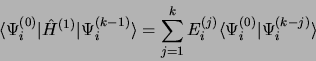 |
(3.50) |
comme 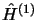 est hermitique
est hermitique
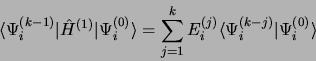 |
(3.51) |
donc
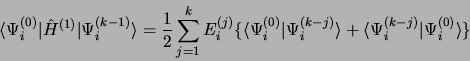 |
(3.52) |
en particulier
La résolution analytique des équations 3.48 n'est pas toujours
possible. Pour résoudre on utilisera le fait que les fonctions propres
de l'opérateur hermitique 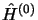 forment une base complète sur
laquelle on peut projeter
forment une base complète sur
laquelle on peut projeter
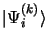 . En introduisant le
projecteur
. En introduisant le
projecteur
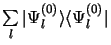 dans
3.48 il vient
dans
3.48 il vient
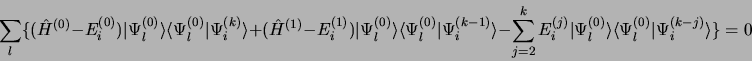 |
(3.55) |
Au premier ordre
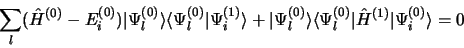 |
(3.56) |
donc
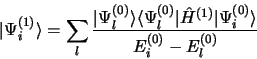 |
(3.57) |
et
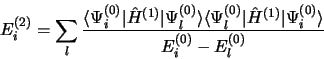 |
(3.58) |



suivant: États dégénérés
monter: Perturbations statiques.
précédent: Perturbations statiques.
Bernard Silvi
2005-03-16
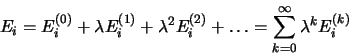
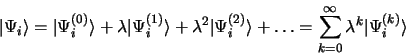
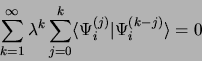
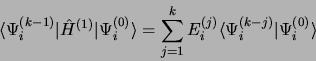
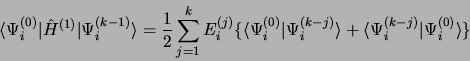
![]() forment une base complète sur
laquelle on peut projeter
forment une base complète sur
laquelle on peut projeter
![]() . En introduisant le
projecteur
. En introduisant le
projecteur
![]() dans
3.48 il vient
dans
3.48 il vient