


suivant: Perturbation dépendant du temps.
monter: Perturbations statiques.
précédent: États dégénérés
Exemple : l'effet Stark
Si un atome d'hydrogène est soumis à un champ électrique externe, la
fréquence de la transition Lyman-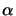 (
(
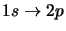 ) est
déplacée d'une quantité proportionelle au champ électrique, pour des
intensités de champ inférieures à 10
) est
déplacée d'une quantité proportionelle au champ électrique, pour des
intensités de champ inférieures à 10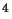 kilovolts/m.
kilovolts/m.
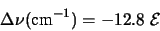 |
(3.68) |
L'intensité du champ électrique est exprimée en kilovolts/m. Pour des
champs plus intenses des effets non-linéaires apparaissent.
La théorie des perturbations au premier ordre permet d'expliquer ce
phénomène quantitativement. Le potentiel de perturbation est
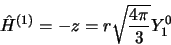 |
(3.69) |
et 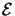 est assimilé au paramètre de perturbation.
La correction au premier ordre de l'énergie de l'état
est assimilé au paramètre de perturbation.
La correction au premier ordre de l'énergie de l'état 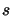 est
est
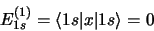 |
(3.70) |
Le niveau 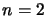 est dégénéré, si l'on choisit d'orienter le champ
électrique suivant
est dégénéré, si l'on choisit d'orienter le champ
électrique suivant 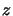 , seuls les éléments de matrice
, seuls les éléments de matrice
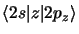 et
et
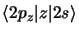 ne sont pas nuls,
ils sont égaux à 3 u.a. La diagonalisation de la matrice
ne sont pas nuls,
ils sont égaux à 3 u.a. La diagonalisation de la matrice 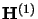 est immédiate et
est immédiate et
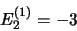 |
(3.71) |
donc
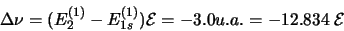 |
(3.72) |
quand 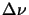 est exprimé en cm
est exprimé en cm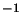 et
et 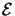 en kvolt/m.
en kvolt/m.



suivant: Perturbation dépendant du temps.
monter: Perturbations statiques.
précédent: États dégénérés
Bernard Silvi
2005-03-16