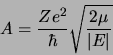suivant: Fonctions radiales des hydrogénoïdes
monter: L'atome d'hydrogène et les
précédent: Expression du laplacien en
Les fonctions propres de 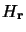 sont également fonctions propres de
sont également fonctions propres de
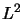 et de l'une des composantes de
et de l'une des composantes de 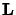 .
.
Les fonctions propres de 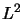 et de
et de 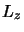 sont les harmoniques sphériques et
les fonctions propres de
sont les harmoniques sphériques et
les fonctions propres de 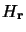 s'expriment sous la forme du produit d'une
harmonique sphérique par une fonction radiale :
s'expriment sous la forme du produit d'une
harmonique sphérique par une fonction radiale :
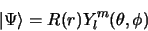 |
(2.103) |
La fonction 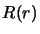 est solution de l'équation différentielle obtenue par
substitution
est solution de l'équation différentielle obtenue par
substitution
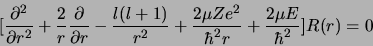 |
(2.104) |
Cette équation ainsi que ses solutions dépendent paramétriquement de 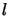 .
Pour les distinguer on les notera
.
Pour les distinguer on les notera 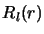 .
.
Les solutions satisfaisantes sont celles pour lesquelles 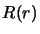 reste fini
pour toutes les valeurs de
reste fini
pour toutes les valeurs de 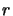 , en effet,
, en effet,
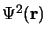 est la probabilité
de présence de l'électron dans l'élément de volume
est la probabilité
de présence de l'électron dans l'élément de volume 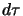 et est donc
borné par 0 et 1.
et est donc
borné par 0 et 1.
Pour résoudre on utilise la fonction intermédiaire 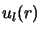
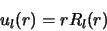 |
(2.105) |
qui permet d'éliminer le terme du premier ordre dans l'équation
différentielle
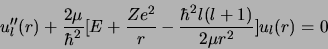 |
(2.106) |
quand
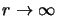 l'équation différentielle tend vers
l'équation différentielle tend vers
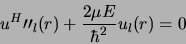 |
(2.107) |
et 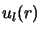 tend vers
tend vers
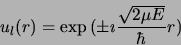 |
(2.108) |
Suivant le signe de 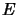 on a deux cas possibles
on a deux cas possibles
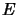 est positif
est positif
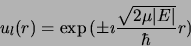 |
(2.109) |
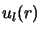 est fini pour toute valeur de
est fini pour toute valeur de 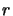 et
et
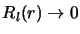
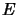 est négatif
est négatif
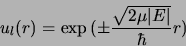 |
(2.110) |
seule l'exponentielle décroissante est physique car
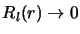 dans ce cas et
dans ce cas et
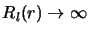 pour l'exponentielle
croissante.
pour l'exponentielle
croissante.
Toutes les valeurs positives de l'énergie sont permises, on a un continuum
(spectre continu de valeurs propres). Ce cas correspond à celui de
l'électron libre. Dans le cas où 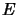 est négatif on doit faire un
ajustement.
On posera
est négatif on doit faire un
ajustement.
On posera
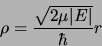 |
(2.111) |
et l'on exprimera 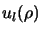 sous forme d'un produit
sous forme d'un produit
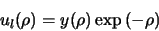 |
(2.112) |
Après simplification par 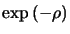 , il vient
, il vient
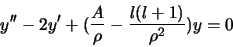 |
(2.113) |
avec
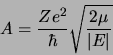 |
(2.114) |
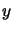 est développé en série de
est développé en série de 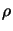
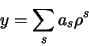 |
(2.115) |
et l'équation différentielle devient
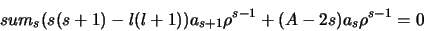 |
(2.116) |
qui doit être vérifiée pour toutes les puissances de 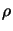 ce qui conduit à la relation de récurrence entre les coefficients
ce qui conduit à la relation de récurrence entre les coefficients 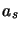
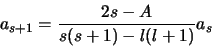 |
(2.117) |
Si l'on a un nombre fini de termes, 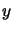 est un polynôme dont le produit par
est un polynôme dont le produit par
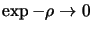 quand
quand
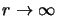 , par contre si l'on a une
série infinie
, par contre si l'on a une
série infinie
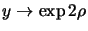 . Pour avoir une solution physique,
on doit avoir un polynôme donc à partir d'un indice
. Pour avoir une solution physique,
on doit avoir un polynôme donc à partir d'un indice 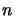 donné les
coefficients
donné les
coefficients
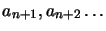 doivent être identiquement nuls, ce qui
implique
doivent être identiquement nuls, ce qui
implique
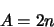 |
(2.118) |
avec 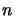 entier. L'énergie
entier. L'énergie 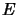 ne peut donc prendre que des valeurs
discrètes, le spectre des valeurs propres est discret : l'énergie est
quantifiée.
ne peut donc prendre que des valeurs
discrètes, le spectre des valeurs propres est discret : l'énergie est
quantifiée.
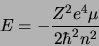 |
(2.119) |
Sous-sections



suivant: Fonctions radiales des hydrogénoïdes
monter: L'atome d'hydrogène et les
précédent: Expression du laplacien en
Bernard Silvi
2005-03-16
![]() reste fini
pour toutes les valeurs de
reste fini
pour toutes les valeurs de ![]() , en effet,
, en effet,
![]() est la probabilité
de présence de l'électron dans l'élément de volume
est la probabilité
de présence de l'électron dans l'élément de volume ![]() et est donc
borné par 0 et 1.
et est donc
borné par 0 et 1.
![]()