


suivant: Résolution de l'équation de
monter: L'atome d'hydrogène et les
précédent: Séparation des mouvements.
Le potentiel est fonction de la seule variable 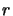 , il est donc avantageux de
travailler dans un système de coordonnées où
, il est donc avantageux de
travailler dans un système de coordonnées où 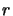 est une variable
explicite. On choisit donc le système des coordonnées sphériques
est une variable
explicite. On choisit donc le système des coordonnées sphériques
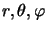 où :
où :
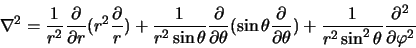 |
(2.99) |
On rapprochera la partie angulaire de cet opérateur de l'expression de
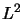
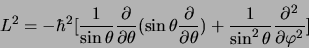 |
(2.100) |
Ce qui permet d'écrire
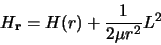 |
(2.101) |
Bernard Silvi
2005-03-16