


suivant: Expression du laplacien en
monter: L'atome d'hydrogène et les
précédent: L'atome d'hydrogène et les
Pour un système comprenant deux particules on séparera le mouvement
du centre de gravité du mouvement relatif des deux particules dans un
référentiel lié au centre de gravité.
On considère deux particules de masse 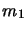 et
et 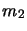 repérées
par les vecteurs position
repérées
par les vecteurs position 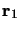 et
et 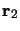 et soumises à un
potentiel d'interaction
et soumises à un
potentiel d'interaction
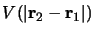 , on
désignera par
, on
désignera par 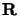 le vecteur position du centre de gravité
le vecteur position du centre de gravité
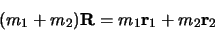 |
(2.92) |
L'équation de Schrödinger dépendant du temps s'écrit:
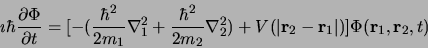 |
(2.93) |
On pose
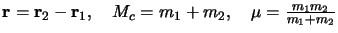
Après avoir exprimé 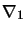 et
et 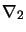 en fonction de
en fonction de
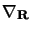 et de
et de
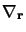 il vient:
il vient:
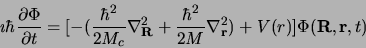 |
(2.94) |
Pour résoudre on posera
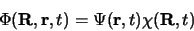 |
(2.95) |
et on résoudra séparément
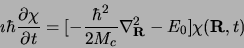 |
(2.96) |
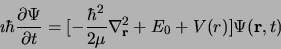 |
(2.97) |
Sans perte de généralité la constante de séparation 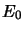 peut
être choisie nulle.
Dans le cas des hydrogénoïdes
peut
être choisie nulle.
Dans le cas des hydrogénoïdes
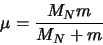 |
(2.98) |



suivant: Expression du laplacien en
monter: L'atome d'hydrogène et les
précédent: L'atome d'hydrogène et les
Bernard Silvi
2005-03-16
![]() et
et ![]() repérées
par les vecteurs position
repérées
par les vecteurs position ![]() et
et ![]() et soumises à un
potentiel d'interaction
et soumises à un
potentiel d'interaction
![]() , on
désignera par
, on
désignera par ![]() le vecteur position du centre de gravité
le vecteur position du centre de gravité
![]() et
et ![]() en fonction de
en fonction de
![]() et de
et de
![]() il vient:
il vient: