Exemple de brisure de symétrie

Il faut préciser que je ne considère que des systèmes à couches fermées, pour éviter les difficultés dues aux différents couplages de spins célibataires. Pour un anneau d'atomes d'hydrogène équidistants comme exemple d'étude, il est possible de définir une maille élémentaire en regroupant deux noyaux avec leurs électrons. Nous utilisons une base minimale d'une fonction atomique $1s$ par atome.[2]La distance interatomique de $0.7474$Å correspond au minimum de l'énergie Hartree-Fock dans la base minimale pour la molécule H$_2$.

Il y a deux possibilités de choix d'orbitales de départ : les deux électrons sont soit sur la liaison à l'intérieur de la maille élémentaire, soit sur l'un des atomes de la maille (alternance entre des ions H$^+$ et H$^-$). Dans les deux cas, les itérations par l'IC des monoexcités produisent une fonction d'onde Hartree-Fock d'une symétrie réduite, qui garde le caractère des orbitales initiales (publication [11]). Pour construire une solution avec la symétrie correcte il faut superposer une solution avec son équivalent centré sur l'atome voisin. Les trois solutions différentes correspondent à des structures différentes de la matrice de la densité, dont je montre un morceau comprenant deux mailles à deux atomes :

$$\underbrace{\pmatrix{a & b & & \cr b & a & & \cr & & a & b \... ...& & a & b \cr & & b & c \cr}}_{\text{centr\'e sur un atome}}$$ (6)

true cm

$$\vbox{\hfil\hskip -1 true cm\epsfysize =1.2 true cm \epsffile {symbris.eps}\hfill}$$

Figure 3: Energie des trois solutions Hartree-Fock pour des anneaux d'atomes d'hydrogène en base minimale. SA est la solution symétrique, avec un électron par atome, et AC-SB et BC-SB sont des solutions à symétrie brisée, avec deux électrons centrés sur un atome (atom centered symmetry broken) ou sur une liaison sur deux (bond centered symmetry-broken). D'après la publication [11].

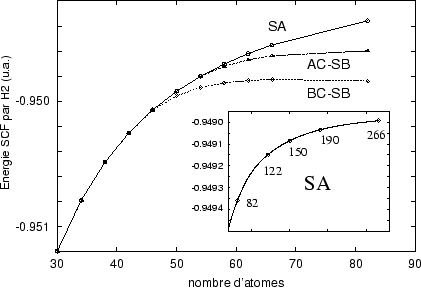Les deux solutions Hartree-Fock à symétrie brisée ont des énergies plus basses que la solution représentant la symétrie de la molécule. L'effet ne se manifeste qu'à partir d'une certaine taille; pour des petits anneaux les trois points de départ amènent au même résultat.[3]Les brisures de symétrie ainsi que des conditions de stabilité ont été formulées par Thouless[#!Thouless!#] et détaillé par Paldus et Cizek dans une série d'articles dans les années 1970.[#!CizekPaldus!#]

Nous voyons ainsi que l'approche choisie pour resoudre les équations Hartree-Fock nous laisse la liberté d'obtenir des solutions dont la nature peut être anticipée; nous ne sommes pas forcés dans l'une ou dans l'autre solution par la procédure.

La brisure de symétrie est un artefact de la méthode Hartree-Fock due à la non-linéarité des équations. Pour obtenir un état fondamental de la symétrie de la molécule, il faut considérer la corrélation électronique, c'est à dire aller au delà de l'approximation Hartree-Fock. Mais même la perturbation au quatrième ordre (MP4) ou la sommation infinie des diagrammes de perturbation des diexcités (LCCD ou CEPA-0) ne suffisent pas à retrouver une solution unique.[4]Nous n'avons pas encore besoin d'une approche spécifique à la corrélation dans les solides, un calcul en orbitales canoniques par un programme standard suffit.

true cm

Figure 4: L'énergie de corrélation (gauche) et l'énergie totale pour les trois solutions Hartree-Fock différentes, d'après la publication [11]. Le calcul des énergies est fait en orbitales canoniques. Même si l'énergie Hertree-Fock ne diffère que peu pour H$_{42}$ ou H$_{46}$ entre les différentes solutions (voir Fig. 3), l'énergie de corrélation peut avoir des variations plus importantes.

Les méthodes Monte Carlo peuvent donner une nouvelle ouverture vers ce genre de problématiques, puisqu'à partir d'une fonction d'onde approximative la variante Diffusion Monte Carlo (DMC) est en principe capable d'extraire la fonction d'onde de l'état fondamental et son énergie totale avec grande précision. La source principale d'erreurs systématiques est la position des nuds (endroits dans l'espace $\{\vec{\rm r}_1\ldots\vec{\rm r}_{n}\}$, où la fonction d'onde est égale à zéro) de la fonction d'onde de départ. Avec les trois solutions Hartree-Fock différentes, nous aurions une estimation de l'erreur liée à la contrainte d'utiliser des nuds (fixés à priori) de la fonction d'onde de départ pour la simulation DMC.

Un autre exemple de brisures de symétrie, cette fois plus réaliste que celui observé dans les systèmes fictifs tels que des anneaux d'hydrogène, sont les modifications tridimensionnelles du phosphore, où dans une structure cubique les trois électrons de valence de chaque atome s'apparient pour former des solides déformés et isolants (phosphore violet de Hittorf ou phorphore noir), ou bien se délocalisent pour former la structure électronique du phosphore métallique dans une structure cubique.

Dans les publications [6], [7] et [11] la construction des orbitales localisées est décrite en détail, pour des anneaux d'hydrogène, métallique et moléculaire, des anneaux d'atomes de béryllium et des hydrocarbures cycliques simples. Des applications à des systèmes réellement étendus ont été présentées dans la publication [14].