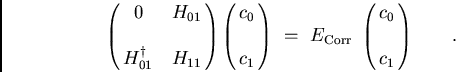 |
(7) |
 |
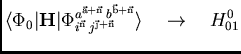 |
(8) |
Il est intéressant d'ajouter des termes
![]() aux éléments
diagonaux
aux éléments
diagonaux
![]() de la matrice
(Eq. 9),
ce qui permet de réécrire le système d'équations aux valeurs propres
sous la forme d'un système linéaire
de la matrice
(Eq. 9),
ce qui permet de réécrire le système d'équations aux valeurs propres
sous la forme d'un système linéaire
Sans habillage (i.e. ![]() ) on obtient les équations CEPA-0,
pour des systèmes périodiques dérivées en 1995 par K. Fink et
V. Staemmler.[#!StaemmlerFink!#] La théorie des hamiltoniens
intermédiaires développée à Toulouse[#!Intermediate!#] amène à
d'autres habillages, qui permettent de retrouver successivement les
différents méthodes CEPA (CEPA-2 et CEPA-3) jusqu'au (SC)
) on obtient les équations CEPA-0,
pour des systèmes périodiques dérivées en 1995 par K. Fink et
V. Staemmler.[#!StaemmlerFink!#] La théorie des hamiltoniens
intermédiaires développée à Toulouse[#!Intermediate!#] amène à
d'autres habillages, qui permettent de retrouver successivement les
différents méthodes CEPA (CEPA-2 et CEPA-3) jusqu'au (SC)![]() CI
(``Self-Consistent Size Consistent CISD'' ou ``Full CEPA'') de la Référence
SCSC. Dans ces cas des déterminants quadriexcités (et au
delà) sont inclus implicitement dans le calcul de l'énergie de
corrélation comme (multiples) produits de coefficients de déterminants
diexcités avec des éléments de la matrice H calculés auparavant :
CI
(``Self-Consistent Size Consistent CISD'' ou ``Full CEPA'') de la Référence
SCSC. Dans ces cas des déterminants quadriexcités (et au
delà) sont inclus implicitement dans le calcul de l'énergie de
corrélation comme (multiples) produits de coefficients de déterminants
diexcités avec des éléments de la matrice H calculés auparavant :
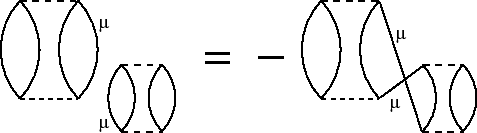 |
Pour l'IC des configurations mono- et diexcitées, le point de départ par
éq. 7, tous les produits de coefficients de déterminants
diexcités
![]() sont retenus sur
la diagonale par l'habillage par
sont retenus sur
la diagonale par l'habillage par
![]() , EPV ou pas, et donc la méthode n'est pas ``size consistent'' en incluant
également des diagrammes non-liés.
, EPV ou pas, et donc la méthode n'est pas ``size consistent'' en incluant
également des diagrammes non-liés.
Pour faire le lien correctement entre l'IC des déterminants diexcités et
les compensations par de déterminants quadiexcités il faut une étape
supplémentaire, correspondant à la réduction d'indices de l'équation
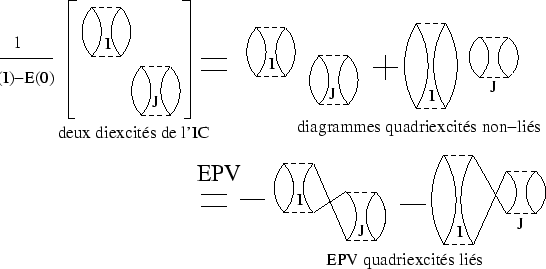
12. Un diagramme de deux diexcités non-liés de l'IC
(modulo le dénominateur ![]() du déterminant
du déterminant ![]() à habiller) peut
être exprimé comme la somme de deux diagrammes quadriexcités non-liés
en utilisant l'identité
à habiller) peut
être exprimé comme la somme de deux diagrammes quadriexcités non-liés
en utilisant l'identité
 |
La preuve au deuxième ordre de perturbation peut être donnée si l'on
regarde le problème deux par deux concernant le déterminant ![]() , habillé
par le déterminant
, habillé
par le déterminant ![]() (nous mettons
(nous mettons
![]() ) :
) :
| (13) |
![\begin{displaymath}
{{H_{0I}^2}\over{H_{II}'}} {{\Delta_I}\over{H_{II}'}} = \...
...J}' H_{I+J,I+J}'}} +
{1\over{H_{II}' H_{I+J,I+J}'}}\right]
\end{displaymath}](img129.gif) |
(14) |
La même logique d'habillage diagonal permet d'acceder à d'autres variantes du calcul de la corrélation, basées sur la matrice de l'hamiltonien, telles que ACPF, AQCC et CCSD.[#!Pepe!#] Les habillages différents sont donnés dans les tableaux I et II.
Le fait, que l'expression de l'habillage repose sur des éléments de
matrice calculés auparavant, rend les méthodes CEPA particulièrement
intéressantes : on somme à l'infini des séries de diagrammes de
perturbation d'ordre et de dégré d'excitation élevé, dans lesquelles
se trouvent des indices d'orbitales en commun. Ceci n'introduit que des
diagrammes liés et utilisables pour des systèmes périodiques avec une
croissance correcte avec la taille du système. L'habillage par le (SC)![]() CI
ou Full CEPA inclut la totalité de ces diagrammes à construire sans
évaluation nouvelle d'éléments de H. En étant capable de
resoudre les équation CEPA-0, nous pouvons inclure alors avec peu d'éffort
supplémentaire un grande partie de la corrélation électronique issue des
diagrammes EPV liés.
CI
ou Full CEPA inclut la totalité de ces diagrammes à construire sans
évaluation nouvelle d'éléments de H. En étant capable de
resoudre les équation CEPA-0, nous pouvons inclure alors avec peu d'éffort
supplémentaire un grande partie de la corrélation électronique issue des
diagrammes EPV liés.
Deux remarques importantes :
La publication [14] décrit les différents habillages et présente des applications aux anneaux d'hydrogène et de LiH, ainsi qu'à un cristal tridimensionnel de béryllium dans une structure cubique simple. Dans le cas de l'hydrogène les habillages par l'ACPF reproduisent presque un calcul d'IC complet. Cependant dans le calcul du cristal infini de Be nous avons montré que les queues des orbitales, mêmes occupées, sont relativement étendues, même pour ce système à couches fermées et dans une base relativement petite.
Il est donc possible de calculer l'énergie de corrélation d'un solide, à condition de disposer d'orbitales localisées, et orthogonales. Mais les applications sont très exigeantes en temps de calcul, et il sera souhaitable de pouvoir exploiter la symétrie du solide au delà de la symétrie translationelle.
Récemment, la localisation de Boys a connu une véritable renaissance dans la communauté des physiciens grâce à l'article de N. Marzari et D. Vanderbilt,[#!MarzariVanderbilt!#] où cette localisation est appliquée aux systèmes périodiques. De même, les groupes travaillant avec des développements en ondes planes, sont intéressés par des jeux d'orbitales moléculaires transférables d'un système à un autre, comme lorsque dans les calculs de type Hückel on identifie des liaisons C-H, C-C et C=C des hydrocarbures. Actuellement, l'équipe de Turin incorpore la localisation de Boys/Marzari-Vanderbilt dans la nouvelle version de CRYSTAL afin de traiter la corrélation, à l'aide d'orbitales virtuelles non-orthogonales.[#!Schutz!#]