Construction des orbitales localisées

Un calcul Hartree-Fock (ou sans interaction biélectronique explicite : Extended Hückel) fournit généralement des orbitales moléculaires complètement délocalisées, $\phi_i$, en diagonalisant l'opérateur de Fock F avec des valeurs propres $\epsilon_i$ ; ces orbitales sont développées sur des orbitales atomiques $\chi_\alpha$ locales

$$\phi_i=\sum_{\alpha} c_{\alpha i} \chi_\alpha\qquad {\text{avec}}\qquad {\bf F} \phi_i = \epsilon_i \phi_i\qquad .$$ (1)

La fonction d'onde $\Psi(\vec{\rm r}_1, \vec{\rm r}_2, \ldots, \vec{\rm r}_n, \sigma_1, \ldots, \sigma_n)$ étant construit par un déterminant en fonction des positions des électrons $\vec{\rm r}_i$ et de leurs spins $\sigma_i$

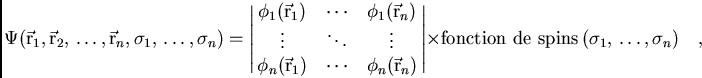$$\Psi(\vec{\rm r}_1, \vec{\rm r}_2, \ldots, \vec{\rm r}_n, ... ...text{fonction de spins} (\sigma_1, \ldots,\sigma_n) \quad ,$$ (2)

les orbitales peuvent être localisées -- a posteriori -- par une transformation unitaire à l'aide d'une fonctionnelle ou par projection, sans changer cette fonction d'onde. La recherche des méthodes de localisation soit pour interpreter le sens chimique des orbitales soit pour rendre les calculs de corrélation moins long amenait au développement de plusieurs voies différentes dont je présenterai une sélection -- un article de revue plus complet est par exemple la réference RamirezSolis.

S. F. Boys décrit en 1960 une méthode de localisation,[#!Boys!#] qui essaie de maximiser la distance moyenne entre les barycentres des orbitales. Dans le même article Boys démontre déjà que la solution obtenue n'est pas toujours unique : il existe par exemple un ensemble continu de solutions pour les orbitales de valence d'une molécule de benzène. Dans une molécule de monoxyde de carbone, trois orbitales de forme ``bananoïde'' représentent la triple liaison $\vert$C$\equiv$O$\vert$. Par contre, les paires libres d'électrons se localisent comme le prévoit le modèle VSEPR de Gillespie[#!Gillespie!#] et al., et l'on retrouve des concepts généraux de la chimie. Il y a un petit prix à payer pour localiser : pour déterminer les barycentres des orbitales il faut disposer des intégrales du moment dipolaire $\langle\chi_\alpha\vert\vec{\rm r}\vert\chi_\beta\rangle$, en plus des intégrales utilisés pour le calcul Hartree-Fock.

Une autre méthode, dont nous nous servirons également par la suite, a été proposée par J. Pipek et P. Mezey.[#!PipekMezey!#] Elle vise à minimiser la fragmentation des orbitales sur les différents centres atomiques. Puisque les fragmentations sont l'inverse des populations $p_\alpha = \sum_\gamma P_{\alpha\gamma}S_{\gamma\alpha}$ cette localisation n'utilise que la matrice de densité $P_{\alpha\beta}=2 \sum_{i\in occ.} c_{\alpha i} c_{\beta i}$ et les intégrales de recouvrement $S_{\alpha\beta}=\langle\chi_\alpha\vert\chi_\beta\rangle$. Les deux matrices, $S$ et $P$, sont d'habitude disponibles et utilisées dans le calcul de la fonction d'onde, ce qui fait qu'il n'y a pas d'intégrales supplémentaires à évaluer. La localisation Pipek-Mezey respecte bien les séparations en orbitales $\pi$ et $\sigma$ des liaisons triples, mais elle ne fournit plus des paires libres séparées. En effet dans le cas d'une molécule possédant plusieurs paires libres comme H$_2$O il n'y a aucune raison que les paires libres occupent des endroits différents autour du même centre atomique (modulo des éléments de symétrie).

Figure 1: Les deux orbitales de la molécule H$_2$O représentant les deux paires libres autour de l'atome d'oxygène.

Les deux méthodes, en partant d'un ensemble d'orbitales canoniques et orthonormées, produisent par des rotations deux à deux des orbitales localisées, également orthonormées.[2]Une généralisation de la méthode de Boys est élaborée par S. Liu et al.[#!Liu!#] en levant cette contrainte d'orthonormalité.

Une alternative aux méthodes a posteriori comme celle de Boys ou Pipek-Mezey est d'inclure la localisation dès la première itération de la solution des équations Hartree-Fock. Ceci est possible par la méthode ``Super-CI'',[#!MCSCF!#] mise au point à Toulouse (Réf. Daudey et publication [7],[3]Les réferences entre crochets [ ] sont détaillées dans la partie V : Publications et ne figurent pas dans la liste des références à la fin de l'exposé des travaux. et indépendamment à Tokyo par T. Sano et O. Matsuoka[#!Sano!#]), applicable non seulement à des systèmes moléculaires, mais également aux systèmes périodiques, à condition d'introduire quelques approximations.

Avant de décrire l'approche ``Super-CI'', nous devons mentionner l'inclusion d'un potentiel de localisation par projection dans la matrice Fock d'un système périodique, proposée par A. Shukla et al.[#!Shukla!#] L'idée est d'ajouter à l'opérateur de Fock de la maille élémentaire des projecteurs sous forme de multiplicateurs de Lagrange, qui introduisent la condition d'orthogonalité des orbitales de la maille élémentaire aux orbitales des mailles voisines. En diagonalisant cet opérateur de Fock modifié, on obtient des orbitales ``canoniques'' de la maille élémentaire, seulement délocalisées à l'intérieur de cette maille. La périodicité est prise en compte, à la fois dans les projecteurs et dans les sommations infinies des intégrales de Coulomb et d'échange lors de la construction de l'opérateur de Fock. Les applications publiées concernent le trans-polyacétylène (1D) et LiF et LiH (3D).[#!ShuklaII!#]

Revenons à la méthode ``Super-CI'', qui introduit une voie alternative de construction des orbitales localisées sans passage par les fonctions de Bloch : l'idée centrale est de baisser l'énergie totale d'un déterminant donné par une interaction de configurations dans l'espace des configurations mono-excitées et de construire un schéma d'itération par deux approximations :

• le développement sur les déterminants $\Psi = \Phi_0 + \sum_{i a} c_i^a \Phi_i^a$ est approchée au premier ordre par une correction des orbitales moléculaires avec les coefficients de l'IC :
  

  $$\tilde{\phi}_i = \phi_i + \sum_a c_i^a \phi_a ; \tilde{\phi}_a = \phi_a - \sum_a c_i^a \phi_a$$ (3)

  
  
  $\phi_i$ réprésente une orbitale occupée (ou ``trou'') et $\phi_a$ une orbitale virtuelle (ou ``particule'').
• les intégrales biélectroniques autre que celles intervenant dans l'opérateur de Fock sont négligées.

La première approximation assure que l'on reste dans la recherche d'une solution Hartree-Fock en corrigeant les orbitales itération par itération jusqu'à ce que les corrections apportées par l'IC des mono-excitations soient négligeables. Ce critère de convergence exploite le théorème de Brillouin, disant que seulement un déterminant Hartree-Fock n'a pas d'interaction avec ses configurations mono-excitées.

La deuxième approximation permet de rendre le calcul aussi efficace qu'une diagonalisation directe de l'opérateur de Fock, mais avec la possibilité d'obtenir directement des orbitales localisées à partir d'un jeu d'orbitales localisées approchées. Si par exemple les orbitales de départ sont issues d'un calcul en base minimale ou construites ``à priori'', la solution obtenue à la fin des itérations conserve le plus possible leur caractère initial. Un avantage supplémentaire tient à ce que la procédure peut être facilement appliquée aux systèmes étendus, en cherchant des orbitales moléculaires centrées dans une maille élémentaire, avec des queues décroissantes sur les mailles voisines. Dans les molécules, l'orthogonalité entre orbitales occupées et orbitales virtuelles est assurée dès le départ, parce que les corrections $\tilde{\phi}_i = \phi_i + \sum_{a} c_{ia}\phi_a$ pour les occupées et $\tilde{\phi}_a = \phi_a - \sum_{i} c_{ia}\phi_i$ pour les virtuelles laissent les deux espaces bien séparés. Par contre, dans un système étendu avec les orbitales localisées dans des mailles $\vec{\rm g}$, soit l'orthogonalité soit la symétrie translationnelle sont détruites par la génération simultanée des nouveaux coefficients des orbitales occupées et virtuelles :

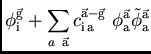$$\tilde{\phi}_{\rm i}^{\vec{\rm g}} = \phi_{\rm i}^{\vec{\rm g}} + \sum_{a \vec{\rm a}} c_{\rm i a}^{... ...\vec{\rm g}} \phi_{\rm a}^{\vec{\rm a}} \cr \tilde{\phi}_{\rm a}^{\vec{\rm a}}$$ (4)

Pour conserver la symétrie translationnelle il faut considérer uniquement les coefficients des fonctions de base de la maille d'origine $\tilde{\phi}_{\rm a}^{\vec{\rm a}} = \phi_{\rm a}^{\vec{\rm a}} - \sum_{i} c_{\rm i a}^{\vec{0}} \phi_{\rm i}^{\vec{0}}$ et orthogonaliser les orbitales à chaque itération. L'orthogonalisation est effectuée par un processus iteratif, utilisant le développement en série de la matrice ${\bf S}^{-1/2}\approx {\bf 1} - {1\over 2}{\bf S}$. Le calcul direct par inversion est impossible parce que S est d'ordre infini.

Avant d'aborder le problème de la corrélation dans les systèmes périodiques tridimensionnels infinis, il me semblait plus raisonnable de développer les méthodes de corrélation dans des molécules périodiques unidimensionnelles et limitées dans l'espace. Les conditions aux limites cycliques (ou de Born-von Karmann) utilisées dans tout les calculs périodiques infinis doivent être également satisfaites par des chaînes fermées en anneaux, même de petite taille. Un atome aussi peut être vu comme un anneau, moins trivialement un dimère. Une fois les méthodes établies pour ces applications, la généralisation aux systèmes infinis semble directe, puisqu'on peut toujours énombrer les mailles d'un réseau infini, partant d'une maille de référence. Le passage d'un anneau à un système tridimensionnel infini se fait en changeant le nombre et les indices des mailles voisines de la maille de référence.

true cm

Figure 2: Passage d'un atome vers un système multidimensionnel en changeant le voisinage de la maille de référence 0.

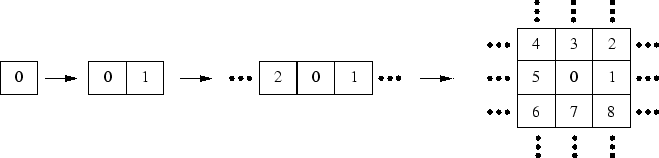Le jeu d'orbitales centré sur la maille de référence détermine alors toutes les orbitales moléculaires du système périodique, les coefficients de développement sur les orbitales atomiques portant de plus un indice de maille $\vec{\rm g}$ :

$$\phi_i = \sum_{\alpha\vec{\rm g}} c_{\alpha i}^{\vec{\rm g... ...{\vec{\rm g}} \chi_{\alpha}^{\vec{\rm g}+\vec{\rm n}} \qquad .$$ (5)

En introduisant des rayons de coupure dans les indices $\vec{\rm g}$ et dans les éléments de la matrice Fock, ainsi que dans la matrice d'IC dont on veut déterminer la valeur propre la plus basse, les itérations sont effectuées avec les étapes suivantes :

• orthogonalisation des orbitales occupées entre elles, occupées et virtuelles, et virtuelles entre elles,
• construction de la matrice Fock,
• construction et détermination de la valeur propre la plus basse de la matrice d'IC des mono-excitées.
• correction des orbitales moléculaires par les coefficients du vecteur propre de l'IC (éq. 3).

On obtient ainsi une solution Hartree-Fock. Pour les systèmes infinis, la construction de la matrice Fock nécessite des sommations infinies -- implémentées par exemple dans le programme CRYSTAL.[#!CRYSTAL!#] Les autres étapes impliquent des routines d'algèbre linéaire standard ou de diagonalisation itérative par la méthode de Davidson.[#!DavidsonIter!#]