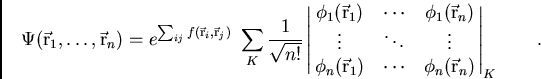 |
(28) |
L'élément central d'un calcul Monte Carlo Quantique est le calcul de la
valeur moyenne d'un
opérateur sur la fonction d'onde. Cette dernière est généralement
écrite comme un produit d'un préfacteur
exponentiel dit de Jastrow décrivqnt explicitement la corrélation
électronique puis
d'une partie déterminantale calculée à partir des
orbitales moléculaires :
Il y a deux possibilités intéressantes d'introduire des orbitales localisées :
Ici nous examinons que la première possibilité d'exploiter la localisation des orbitales, la deuxième étant relativement facile à mettre en place[#!Luchow!#] grâce à des bibliothèques de programmes comme SPARSE ou UMFPACK, qui sont librement accessibles.
L'énergie totale est calculée par des méthodes Monte-Carlo Quantique à
partir d'une une énergie locale ![]() par
par
avec une distribution de probabilité donné par
![]() . Les positions des électrons evoluent à partir d'un
choix initial d'une configuration x à une autre x' avec des
probabilités de transition obéissant à la condition de la balance
détaillée d'après l'algorithme de Metropolis et al.[#!Metropolis!#] :
. Les positions des électrons evoluent à partir d'un
choix initial d'une configuration x à une autre x' avec des
probabilités de transition obéissant à la condition de la balance
détaillée d'après l'algorithme de Metropolis et al.[#!Metropolis!#] :
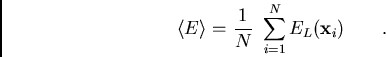 |
(31) |
Si ![]() était fonction propre de H, la valeur propre
correspondante de l'équation de Schrödinger donnerait une valeur unique de
l'énergie locale
pour toute configuration des électrons. Sinon, l'énergie totale
de l'équation 29 est minimisée en recherchant des expressions et
des paramètres
optimaux, soit du facteur de Jastrow et de la fonction de corrélation
était fonction propre de H, la valeur propre
correspondante de l'équation de Schrödinger donnerait une valeur unique de
l'énergie locale
pour toute configuration des électrons. Sinon, l'énergie totale
de l'équation 29 est minimisée en recherchant des expressions et
des paramètres
optimaux, soit du facteur de Jastrow et de la fonction de corrélation
![]() , soit des paramètres des orbitales en utilisant les
orbitales Hartree-Fock, puis les orbitales naturelles d'un calcul d'IC. On
peut aussi utiliser des fonctions d'ondes multidéterminantales
corrélées, issues des calculs MCSCF, (G)VB ou d'un IC.
, soit des paramètres des orbitales en utilisant les
orbitales Hartree-Fock, puis les orbitales naturelles d'un calcul d'IC. On
peut aussi utiliser des fonctions d'ondes multidéterminantales
corrélées, issues des calculs MCSCF, (G)VB ou d'un IC.
Si l'on veut utiliser des fonctions d'onde corrélées, la localisation permet de condenser les expansions en déterminants, comme nous l'avons demontré dans le premier chapitre. Il est utile de rappeler que ces fonctions d'onde sont toujours des fonctions dans l'espace engendré par le déterminant de référence et ses mono- et di-excités. Les sommation infinies introduites dans le premier chapitre améliorent l'énergie totale vers des calculs CCSD(T), mais la fonction d'onde reste toujours limitée aux di-excitées.
L'équation 29 et l'expression de la probabilité de transition (éq.
30) montrent que ni la normation ni l'orthogonalisation ne sont
nécessaires pour la fonction d'onde ![]() , puisque d'une part la norme
intervient dans l'expression de l'énergie et d'autre part la partie du
déterminant de la fonction d'onde absorbe toute partie de recouvrement des
orbitales.
, puisque d'une part la norme
intervient dans l'expression de l'énergie et d'autre part la partie du
déterminant de la fonction d'onde absorbe toute partie de recouvrement des
orbitales.
Or les localisations de type Pipek-Mezey ou Boys donnent des orbitales
localisées orthogonales, car les optimisations de fonctionnelles se font
par des rotations 2![]() 2, qui ne changent pas les angles entre les
vecteurs. La généralisation de la minimisation sans la contrainte
d'orthogonalisation, donné par Liu et al[#!Liu!#] pour le cas de la
localisation de Boys, pourrait ouvrir une alternative en gardant
l'optimisation d'une fonctionnelle de localisation.
2, qui ne changent pas les angles entre les
vecteurs. La généralisation de la minimisation sans la contrainte
d'orthogonalisation, donné par Liu et al[#!Liu!#] pour le cas de la
localisation de Boys, pourrait ouvrir une alternative en gardant
l'optimisation d'une fonctionnelle de localisation.
Notre but est ici de construire des déterminants en orbitales localisées, non-orthogonales, en utilisant les fonctions d'onde d'un calcul de perturbation ou d'un IC, voire CEPA-0. Les résultats que je vais présenter n'ont pas encore été exploités par un calcul Monte-Carlo Quantique; il s'agit encore d'une étape préparatoire. Nous verrons par la suite l'importance d'une analyse détaillée de cette étape.
La projection à partir de la moitié de la matrice densité à une particule est une méthode relativement directe de construction d'orbitales localisées.[#!Chambaud!#,#!RamirezSolis!#] Les orbitales atomiques étant bien localisées dans l'espace, cette procédure de projection donne des vecteurs le moins délocalisées possibles, sans contrainte de produire des orbitales orthogonales. Pour l'instant nous ne prenons que le déterminant Hartree-Fock, car si nous savons exploiter la localisation pour un déterminant, nous pouvons généraliser la procédure pour une expansion multi-déterminantale, donnant ainsi des coeffcients d'orbitales optimales pour chaque état inclu dans la fonction d'onde.
La projection utilise la matrice densité et la matrice de recouvrement
pour exprimer le projecteur ![]() sur l'espace des orbitales occupées :
sur l'espace des orbitales occupées :
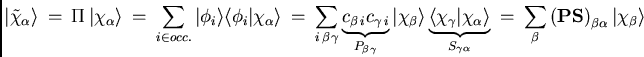 |
(32) |
La projection sur le complément de ![]() ,
,
![]() donne les orbitales virtuelles, les plus localisées possibles, comme
l'ont proposé Pulay et al..[#!Boughton!#] Cette construction de l'espace
virtuel est implementé dans le programme MOLPRO, [#!Hampel!#] avec un
critère de sélection des orbitales : les
orbitales virtuelles projetées autour d'une orbitale occupée sont
retenues, limitant ainsi le nombre d'orbitales virtuelles et évitant des
bases sur-complètes. Dans l'approche Monte-Carlo seules les orbitales
occupées de chaque déterminant sont nécessaires, tandis que la
construction de l'espace des orbitales virtuelles, importantes dans les
méthodes post Hartree-Fock ``classiques'' telles que perturbation ou IC est
inutile.
donne les orbitales virtuelles, les plus localisées possibles, comme
l'ont proposé Pulay et al..[#!Boughton!#] Cette construction de l'espace
virtuel est implementé dans le programme MOLPRO, [#!Hampel!#] avec un
critère de sélection des orbitales : les
orbitales virtuelles projetées autour d'une orbitale occupée sont
retenues, limitant ainsi le nombre d'orbitales virtuelles et évitant des
bases sur-complètes. Dans l'approche Monte-Carlo seules les orbitales
occupées de chaque déterminant sont nécessaires, tandis que la
construction de l'espace des orbitales virtuelles, importantes dans les
méthodes post Hartree-Fock ``classiques'' telles que perturbation ou IC est
inutile.
La projection des orbitales atomiques sur l'espace des orbitales occupées
donne le même nombre de projections que d'orbitales atomiques -- il faut
choisir maintenant ![]() projections sans dépendance linéaire. Pour
cela, les projections sont d'abord rangées selon un critère de
localisation à définir, et la première, la plus localisée, est retenue
comme fonction de départ. Le passage de
projections sans dépendance linéaire. Pour
cela, les projections sont d'abord rangées selon un critère de
localisation à définir, et la première, la plus localisée, est retenue
comme fonction de départ. Le passage de ![]() à
à ![]() projections se fait
par la procédure suivante : la première de la liste des projections non encore
utilisées est ajoutée aux
projections se fait
par la procédure suivante : la première de la liste des projections non encore
utilisées est ajoutée aux ![]() projections déjà sélectionnées. Les
valeurs propres de la matrice des recouvrements des
projections déjà sélectionnées. Les
valeurs propres de la matrice des recouvrements des ![]() projections sont
calculées ensuite. Si la plus petite valeur propre est supérieur à un seuil
choisi auparavant, la projection ajoutée est
retenue; sinon elle est rejetée et la projection suivante de la liste est
prise. A la fin il y a deux possibilités : soit nous avons trouvé
projections sont
calculées ensuite. Si la plus petite valeur propre est supérieur à un seuil
choisi auparavant, la projection ajoutée est
retenue; sinon elle est rejetée et la projection suivante de la liste est
prise. A la fin il y a deux possibilités : soit nous avons trouvé
![]() projections sans dépendances linéaires, soit le seuil choisi
pour décider s'il y a ou non une dépendance linéaire était trop grand
et nous devrons recommencer la procédure avec un seuil plus petit. La
reprise est facilement possible car les projections n'ont pas été
changées par la sélection.
projections sans dépendances linéaires, soit le seuil choisi
pour décider s'il y a ou non une dépendance linéaire était trop grand
et nous devrons recommencer la procédure avec un seuil plus petit. La
reprise est facilement possible car les projections n'ont pas été
changées par la sélection.
Un critère de localisation est obtenu en attribuant à chaque orbitale moléculaire un nombre égal à la somme des valeurs absolues des coefficients, divisé par les coefficient le plus grand :
 |
(33) |
Pour une orbitale délocalisée sur deux centres
![]() nous
trouvons ainsi
nous
trouvons ainsi ![]() , et pour une orbitale parfaitement localisée sur un
seul centre (
, et pour une orbitale parfaitement localisée sur un
seul centre (![]() ou
ou ![]() )
) ![]() . Toute autre
orbitale aura une valeur
. Toute autre
orbitale aura une valeur ![]() entre ces deux limites.
entre ces deux limites.
Nous examinons maintenant plusieurs systèmes : avec des orbitales canoniques, des
orbitales localisées par les méthodes de Boys et de Pipek-Mezey, et
localisées par la méthode des projections que l'on vient de décrire. Les
orbitales obtenues par projections peuvent être orthogonalisées entre
elles, ce qui donne une mesure des délocalisations par l'orthogonalisation
(les queues d'orthogonalisation). Nous utilisons l'orthogonalisation
symétrique par S![]() .
.
Le premier exemple considéré est une chaîne d'atomes d'hydrogène
relativement longue en base minimale, avec des distances interatomiques
alternées de ![]() et
et ![]() , avec
, avec ![]() Å (voir section
IIIB2). En base minimale, avec une
orbitale atomique par atome, nous pouvons visualiser facilement la taille des
coefficients de chaque orbitale moléculaire.
Å (voir section
IIIB2). En base minimale, avec une
orbitale atomique par atome, nous pouvons visualiser facilement la taille des
coefficients de chaque orbitale moléculaire.
Pour des bases comprenant plusieurs orbitales atomiques par centre, une analyse statistique de la taille des coefficients des OA dans les OM peut révéler le degré de localisation des orbitales moléculaires. Si de simples dessins de contours avec échelle logarithmique montrent des détails par orbitale dans l'espace réel, ils ne montrent pas le nombre d'opérations à effectuer pour évaluer l'orbitale moléculaire comme produit de coefficients et de fonctions atomiques.
L'analyse statistique trouve le nombre de coefficients de chaque ordre
de grandeur et un diagramme cumulatif qui indique le nombre de coefficients
-- au dessus d'un seuil à définir -- à retenir pour le calcul
explicite de la fonction d'onde ![]() .
.
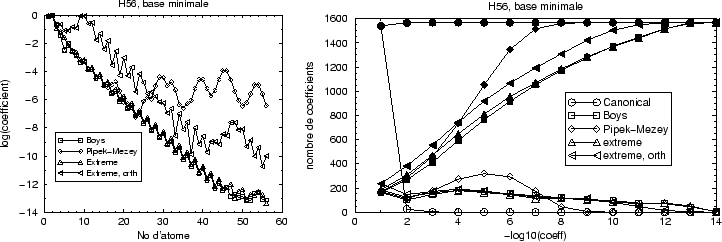
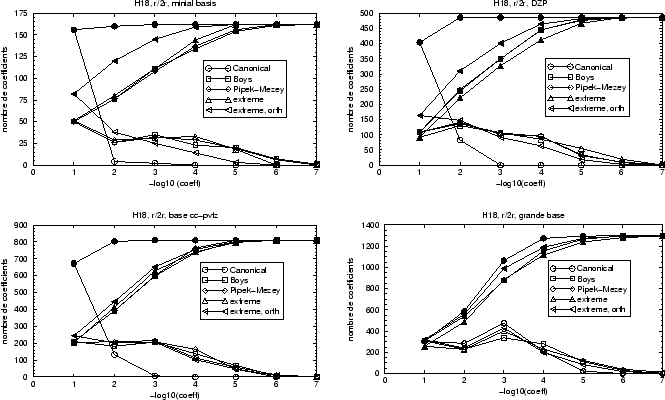
Ces deux analyses (coefficients explicites et analyse statistique) sont
présentées dans la figure 25. La partie gauche présente
des valeurs absolues des coefficients de l'orbitale
``centrée'' sur l'extrémité de la chaîne et montre ainsi la
décroissance exponentielle de l'orbitale dans l'espace. Les orbitales
non-orthogonales, obtenues par projection, sont désormais nommées
``extrême''; ``extrême, orth'' désigne leurs correspondants
orthogonalisées par S![]() . Étonnament les orbitales Boys,
Pipek-Mezey et celles obtenues par projection ont exactement la même
décroissance exponentielle. L'orthogonalisation a posteriori des orbitales
``extrêmes'' délocalise davantage les orbitales que les procédures Boys
et Pipek-Mezey qui conservent l'orthogonalité des orbitales canoniques.
. Étonnament les orbitales Boys,
Pipek-Mezey et celles obtenues par projection ont exactement la même
décroissance exponentielle. L'orthogonalisation a posteriori des orbitales
``extrêmes'' délocalise davantage les orbitales que les procédures Boys
et Pipek-Mezey qui conservent l'orthogonalité des orbitales canoniques.
La partie droite (symboles creux) montre le nombre des coefficients de toutes les orbitales occupées par ordre de grandeur, tandis que les symboles pleins donnent les cumulatifs, par ordre de grandeur. L'ensemble de toutes les orbitales occupées montre, comme l'orbitale centrée sur l'extrémité, que les localisations par la procédure de Boys et par projections ont le même ordre de délocalisation générale.
 |
Nous admettons que la flexibilité des orbitales en base minimale n'est pas très grande, même si l'hamiltonien correct non-relativiste est utilisé dans ce modèle simple.
Que se passe-t-il en agrandissant la base atomique? Le nombre d'orbitales moléculaires occupées est le même. Par contre la densité moléculaire est de mieux en mieux représentée, permettant des polarisations des atomes ``dans la molécule''. Ceci entraîne un grand nombre de coefficients relativement petits dans les expansions des orbitales moléculaires en orbitales atomiques.
D'autre part, la plupart des fonctions de polarisation ne contribue pas à la fonction d'onde parce qu'elles sont d'une symétrie spatiale différente.
Pour limiter l'effort calculatoire nous nous contentons d'une chaîne de 18 atomes d'hydrogène comme exemple.
 |
Dans ce cas le nombre total de coefficients possibles pour l'ensemble des
orbitales occupées est de 9![]() N
N![]() . La symétrie
réduit largement le nombre d'orbitales atomiques utilisées : parmi les
trois orbitales
. La symétrie
réduit largement le nombre d'orbitales atomiques utilisées : parmi les
trois orbitales ![]() seule la
seule la ![]() a la symétrie de la fonction d'onde
tandis que pour les
a la symétrie de la fonction d'onde
tandis que pour les ![]() seules
seules ![]() et
et ![]() utilisées.
utilisées.
Or dans une expansion en déterminants d'une fonction d'onde d'un IC, ces orbitales atomiques non utilisées dans la solution Hartree-Fock peuvent bien contribuer via des diexcitations, dont le produit direct des réprésentations irrductibles des orbitales occupées a la même symétrie que l'état fondamental.
Concernant les localisations différentes nous obtenons plusieurs résultats
en augmentant la base. En base minimale, les localisations Boys,
Pipek-Mezey et ``extrême'' par projection montrent à peu près la même
repartition de taille des coefficients comme l'indiquait
la figure 25. En ajoutant des fonctions de polarisation, les orbitales
canoniques aussi ont également des petits coefficients sur ces fonctions,
comme les
orbitales localisées. La différence en nombre de coefficients importants
entre orbitales localisées et orbitales canoniques disparaît quasiment
pour la base la plus grande utilisée. En ne sélectionnant que
les coefficients plus grand que 10![]() , la localisation de Boys donne toujours
des orbitales aussi localisées que la projection avec orbitales
non-orthogonales. Avec des coefficients un peu plus grands, jusqu'à 10
, la localisation de Boys donne toujours
des orbitales aussi localisées que la projection avec orbitales
non-orthogonales. Avec des coefficients un peu plus grands, jusqu'à 10![]() , la
méthode des projections donne le nombre de coefficients le plus bas.
, la
méthode des projections donne le nombre de coefficients le plus bas.
Orthogonaliser les orbitales extrêmes donne, semble-t-il, des orbitales plus délocalisées que de orbitales orthogonales de Boys ou Pipek-Mezey. Encore une fois, les différences deviennent de plus en plus petites avec l'augmentation des bases atomiques.
Nous voyons alors dans cet exemple que la localisation par projection n'a pas d'avantage évident par rapport aux autres localisations, celles de Boys ou Pipek-Mezey. Dans les super-molécules d'hydrogène, la densité électronique est très faible. Or la localisation mélange les orbitales en conservant la densité totale de la molécule, ce qui ne laisse plus beaucoup de flexilibilité aux orbitales occupées.
Par contre pour des molécules plus riches en électrons, avec des liaisons mêmes multiples, la localisation par projection sans condition d'orthogonalité devrait amener à des orbitales bien plus localisées que les méthodes Boys ou Pipek-Mezey qui préservent l'orthonormalité.
Un exemple d'une bonne taille peut être la molécule C![]() H
H![]() ((1,3,5)hexatriène) -- elle est
étudiée dans la littérature dans le contexte de la réaction de
cyclisation par l'équilibre hexatriène
((1,3,5)hexatriène) -- elle est
étudiée dans la littérature dans le contexte de la réaction de
cyclisation par l'équilibre hexatriène
![]() cyclohexadiène.[#!hexatriene!#] L'état fondamental de cette molécule
est de symétrie C
cyclohexadiène.[#!hexatriene!#] L'état fondamental de cette molécule
est de symétrie C![]() et à couches fermées. La présence de
liaisons conjugées a pour conséquence l'existence d'une multitude
d'états excités (
et à couches fermées. La présence de
liaisons conjugées a pour conséquence l'existence d'une multitude
d'états excités (
![]() ), qui rend le calcul de
l'énergie de corrélation, voire la
spectroscopie théorique de cette molécule, relativement délicat.
), qui rend le calcul de
l'énergie de corrélation, voire la
spectroscopie théorique de cette molécule, relativement délicat.
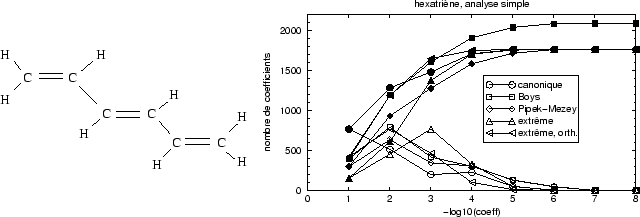 |
La localisation extrême, comme prévu, entraîne une réduction
significative des coefficients de grande taille : environ 250 coefficients ont
des
valeurs absolues comprises entre 0.1 et 1.0, tandis que pour les autres
localisations, Boys, Pipek-Mezey et la localisation par projection après
orthogonalisation le nombre de coefficients de cet ordre de
grandeur est doublé voire triplé. Les orbitales canoniques ont même cinq
fois plus de coefficients supérieurs à 0.1. Si on prend les coefficients
plus grands que 10![]() l'avantage des orbitales
non-orthogonales est moins évident : toutes les méthodes demandent
d'évaluer grosso modo
1800 coefficients d'orbitales, à l'exception de la localisation de Boys pour
laquelle l'expansion d'orbitales en 200 orbitales atomiques
supplémentaires. Ceci
est une conséquence directe de l'absence de la séparation
l'avantage des orbitales
non-orthogonales est moins évident : toutes les méthodes demandent
d'évaluer grosso modo
1800 coefficients d'orbitales, à l'exception de la localisation de Boys pour
laquelle l'expansion d'orbitales en 200 orbitales atomiques
supplémentaires. Ceci
est une conséquence directe de l'absence de la séparation ![]() dans
cette méthode. Au lieu de produire une orbitale
dans
cette méthode. Au lieu de produire une orbitale ![]() et une orbitale
et une orbitale
![]() séparément avec un coefficient important sur les OA de symétrie
séparément avec un coefficient important sur les OA de symétrie
![]() et
et ![]() chacune, il y a deux combinaisons linéaires demandant deux
coefficients pour former
chacune, il y a deux combinaisons linéaires demandant deux
coefficients pour former
![]() et
et
![]() . Dans cet exemple simple il y a donc quatre coefficients importants
au lieu de deux.
. Dans cet exemple simple il y a donc quatre coefficients importants
au lieu de deux.
L'analyse statistique présentée ici est indépendente de toute notion de distance entre orbitales atomiques ou moléculaires, seule la répartition des tailles de coefficients est affichée. Or, dans les configurations à échantillonner dans le calcul Monte Carlo les électrons se déplacent principalement dans les régions de grande densité électronique, et ils sont rarement dans les petites queues loin du barycentre d'une orbitale localisée. En introduisant une fonction d'une forme de chapeau ou cloche autour du barycentre de chaque orbitale moléculaire avant l'analyse statistique, nous pouvons supprimer l'évaluation de petites queues. Par contre au voisinage du barycentre l'orbitale moléculaire est toujours évaluée avec grande précision.
Essayons la possibilité suivante : les coefficients plus grands que
0.01 des orbitales normées sont gardés, mais les coefficients plus
petits sont multipliés (pour l'analyse) par une fonction exponentielle de la
distance entre le barycentre de l'orbitale moléculaire (![]() ) et le
centre de l'orbitale atomique
) et le
centre de l'orbitale atomique
![]() :
:
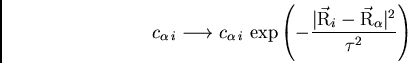 |
(34) |
avec un facteur d'échelle ![]() .
. ![]() u.a. semble être une bonne
valeur, mettant l'échelle globale à env. 1
u.a. semble être une bonne
valeur, mettant l'échelle globale à env. 1![]() Å. On peut également
penser à des rayons van der Waals et définir des facteurs d'échelle
individuels pour chaque atome, ou même séparer orbitales de c
Å. On peut également
penser à des rayons van der Waals et définir des facteurs d'échelle
individuels pour chaque atome, ou même séparer orbitales de c![]() ur
et de valence. Pour l'instant nous présentons des analyses pour une fonction
gaussienne globale.
ur
et de valence. Pour l'instant nous présentons des analyses pour une fonction
gaussienne globale.
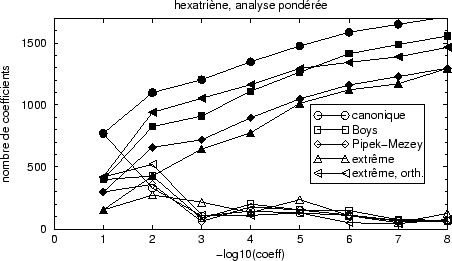 |
Figure 28 montre l'effet de cette analyse statistique
pondérée dans l'exemple du hexatriène. Ajoutons que nous
définissons ainsi un seuil pour décider quels coefficients des
orbitales moléculaires peuvent être négligés sans introduire
d'erreurs sensibles. Pour le calcul Monte Carlo les coefficients
![]() sont utilisés, pas les coefficients pondérés.
sont utilisés, pas les coefficients pondérés.
La localisation des orbitales se fait remarquer maintenant puisque les orbitales canoniques ne semblent plus mieux localisées que les orbitales Boys de la figure 27. Nous voyons aussi qu'après coupure des contributions à petits coefficients et loin du centre les localisations de Pipek-Mezey et par projection deviennent similaires en nombre de coefficients à retenir et à évaluer.
Le résultat global concernant les queues d'orthogonalisation est toujours le même : l'orthogonalisation intrinsèque ne pénalise la localisation au delà de quelques pourcents, par contre l'orthogonalisation après projection délocalise les orbitales.
Considérons maintenant une molécules un peu plus grande, la porphyrine sous sa forme ``base libre'' : cette molécule est consitutée d'élements legers, H, C, et N, avec des délocalisations aromatiques dans les quatre groupes de pyrrole.
 |
Cette molécule présente un interêt biologique car elle est l'unité centrale de l'hémoglobine (le porteur d'oxygène dans le sang). Elle est étudiée actuellement par des méthodes Monte-Carlo Quantique dans le groupe de W. Lester à Berkeley (Californie).[#!Aspuru!#]
Nous nous attendons à des résultats semblables à ceux du
1,3,5-hexatriène, avec séparation ![]() caractérisée par le nombre
élevé de coefficients orbitalaires dans le cas de la localisation de Boys. La
repartition des électrons dans les anneaux ou les ramifications pourrait
introduire plus de contraintes d'orthogonalité que dans une molécule
linéaire comme le hexatriène. Par conséquent, la localisation sans
orthogonalité peut être plus avantageuse.
caractérisée par le nombre
élevé de coefficients orbitalaires dans le cas de la localisation de Boys. La
repartition des électrons dans les anneaux ou les ramifications pourrait
introduire plus de contraintes d'orthogonalité que dans une molécule
linéaire comme le hexatriène. Par conséquent, la localisation sans
orthogonalité peut être plus avantageuse.
Le calcul a été effectué avec les mêmes bases que pour C![]() H
H![]() : une
base 62111/411 pour C et N et 311 pour H, soit en total 378 orbitales
atomiques pour la porphyrine.
: une
base 62111/411 pour C et N et 311 pour H, soit en total 378 orbitales
atomiques pour la porphyrine.
La localisation de Boys implique 1,5 fois plus d'orbitales atomiques dans les
expansions des OM que les autres méthodes, les orbitales canoniques
y comprises. La repartition des tailles de coefficients est similaire à
celle de la hexatriène, à l'exception de la valeur à 10![]() , pour
laquelle les orbitales non-orthogonales par projection demandent maintenant le
moins de coefficients dans le développement.
, pour
laquelle les orbitales non-orthogonales par projection demandent maintenant le
moins de coefficients dans le développement.
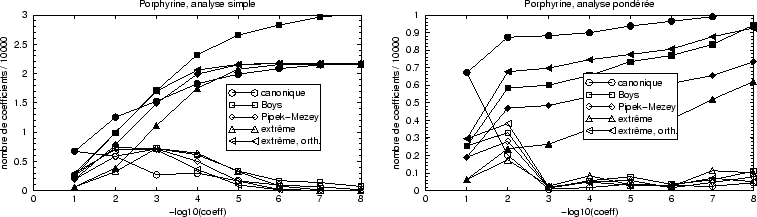 |
L'analyse pondérée montre l'interêt des orbitales projétées dans ce cas d'une grande molécule : le nombre de coefficients à évaluer est faible et représente la moitié de celui nécessité par la localisation Pipek-Mezey. Reste à savoir quel est l'impact sur l'énergie; le tableau IX analyse les conséquences sur l'énergie totale de la troncation des orbitales. Il apparait clairement qu'une bonne convergence est conservée lorsque les petits coefficients sont négligés. Ceci est en accord avec l'idée que les contributions à l'énergie ont un ordre de grandeur voisin du carré des petits coefficients.
La convergence est beaucoup moins bonne en annulant les coefficients moyensqui
correspondent à des des orbitales atomiques centrées loin du barycentre
de l'orbitale moléculaire. L'orbitale 1s d'un atome de carbone par exemple
interagit (faiblement) avec l'orbitale 1s d'un atome voisin, provoquant
peut-être un coefficient de développement de 10![]() ou
ou ![]() . En
négligeant cette petite contribution à zéro, la conséquence sur l'énergie peut
être relativement grande, puisque les orbitales de c
. En
négligeant cette petite contribution à zéro, la conséquence sur l'énergie peut
être relativement grande, puisque les orbitales de c![]() ur sont responsables
de la plus grande partie de l'énergie totale. Nous avons donc gardées des
petites corrections ``sur place'', responsables de la bonne forme de
l'orbitale autour de son barycentre.
ur sont responsables
de la plus grande partie de l'énergie totale. Nous avons donc gardées des
petites corrections ``sur place'', responsables de la bonne forme de
l'orbitale autour de son barycentre.
Bien que cette convergence soit moins rapide que pour l'analyse simple avec
seulement 8![]() % de coefficients non-nuls, l'énergie totale est calculée
à 1
% de coefficients non-nuls, l'énergie totale est calculée
à 1![]() u.a. près, tandis que l'utilisation de
l'analyse simple entraîne une erreur d'env. 20
u.a. près, tandis que l'utilisation de
l'analyse simple entraîne une erreur d'env. 20![]() u.a. sur
l'énergie Hartree-Fock en utilisant 30
u.a. sur
l'énergie Hartree-Fock en utilisant 30![]() % (localisation Pipek-Mezey) ou
13
% (localisation Pipek-Mezey) ou
13![]() % (localisation par projection) des coefficients non nuls.
% (localisation par projection) des coefficients non nuls.
Il est à esperer que l'erreur introduite par les coupures des orbitales peut être compensée par l'introduction du facteur de Jastrow et la méthode Diffusion Monte Carlo.
Les densités de ces deux molécules (hexatriène et porphyrine) sont relativement homogènes à en raison de la délocalisation. Par conséquent, les orbitales occupées et les orbitales vituelles ne sont séparées que par une petite différence d'énergie. Or, la localisation des orbitales doit être difficile dès le début, comme l'a démontré W.Kohn pour des systèmes périodiques unidimensionnels.[#!Kohngap!#] Dans un système périodique une fonction de Wannier, qui est l'équivalent d'une orbitale localisée dans une molécule linéaire ou cyclique, ne montre une décroissance exponentielle qu'avec un exposant proportionel à la difference d'énergie entre orbitales occupées et virtuelles. Notre intention de chercher des molécules avec des fortes densités électroniques de valence nous a mis peut-être sur une mauvaise piste, en regardant des molécules d'un interêt photochimique -- c'est à dire avec un spectre d'excitations de faible énergie.
Néanmoins l'analyse pondérée nous a déjà permis de recalculer l'énergie Hartree-Fock de la porphyrine qu'avec un nombre faible de coefficients non-nuls.
Pour conclure nous appliquons les mêmes analyses à des molécules
beaucoup plus favorables à la localisation par projection : des molécules
saturées dans lesquelles les conceptes de liaisons formées par paires
d'électrons distantes et séparables sont davantage respectés. La figure
31 montre alors les résultats pour deux hydrocarbures simples,
idéalisées, sans ramifications. Les angles sont les angles des
tetraèdres parfaits, et il n'y a que deux longueurs de liaisons : 108![]() pm
pour une liaison C-H et 154
pm
pour une liaison C-H et 154![]() pm pour une liaison C-C.
pm pour une liaison C-C.
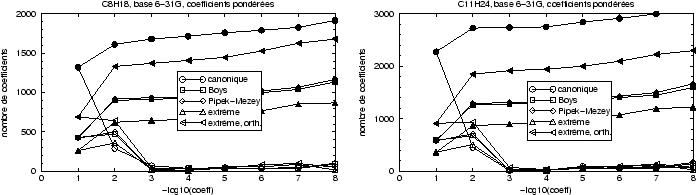 |
Dans cette figure nous remarquons clairement les effets attendus de la localisation. Les localisations de Boys et de Pipek-Mezey donnent à peu près les mêmes repartitions des tailles des coefficients, bien en dessus du nombre de coefficients de taille égale de la localisation par projection. Ceci montre que dans ce cas de molécules saturées les deux méthodes sont à peu près équivalentes.
Pour la molécule C![]() H
H![]() nous arrivons alors à calculer
l'énergie totale à env. 50
nous arrivons alors à calculer
l'énergie totale à env. 50![]() mH près avec seulement 13% de
coefficients non-nuls, ce qui montre encore un fois la possibilité
d'utiliser des localisations d'orbitales dans les méthode Monte Carlo.
mH près avec seulement 13% de
coefficients non-nuls, ce qui montre encore un fois la possibilité
d'utiliser des localisations d'orbitales dans les méthode Monte Carlo.
La procédure décrite au début de ce chapitre est appelé Monte Carlo
Quantique variationnel et vise à optimiser une fonction d'onde inaccessible
par des moyen de la chimie quantique traditionnelle faute de la possibilité
dévaluer les integrales
![]() analytiquement.
L'énergie obtenue est celle de l'équation 29. Il est possible
d'obtenir une équation de diffusion à partir de l'équation de
Schrödinger en projettant sur des temps imaginaires. La résolution de
cette équation permet de calculer l'énergie ``quasi exacte'' de l'état
fondamental du système sans qu'on ait besoin de connaître explicitement
cet état fondamental ou sa fonction d'onde.
analytiquement.
L'énergie obtenue est celle de l'équation 29. Il est possible
d'obtenir une équation de diffusion à partir de l'équation de
Schrödinger en projettant sur des temps imaginaires. La résolution de
cette équation permet de calculer l'énergie ``quasi exacte'' de l'état
fondamental du système sans qu'on ait besoin de connaître explicitement
cet état fondamental ou sa fonction d'onde.
Cette variante de méthode Monte-Carlo,
appellée ``Diffusion Monte Carlo'', serait une méthode de choix, si
elle n'avait un petit défaut : la fonction d'onde ![]() change le signe
en échangeant deux électrons. Or, pour une moyenne stable,
l'échantillonnage doit se faire dans une ``pochette'' dans l'espace des
3
change le signe
en échangeant deux électrons. Or, pour une moyenne stable,
l'échantillonnage doit se faire dans une ``pochette'' dans l'espace des
3![]() coordonnées des
coordonnées des ![]() électrons d'un système, où la fonction d'onde
exacte garde son signe. Malheureusement, la seule information sur le signe
global de
électrons d'un système, où la fonction d'onde
exacte garde son signe. Malheureusement, la seule information sur le signe
global de ![]() nous parvient par la partie déterminantale de la fonction
d'essai, dans notre cas le déterminant Hartree-Fock. En localisant les
orbitales de ce déterminant, et en négligeant des petits coefficients des
orbitales moléculaires, les n
nous parvient par la partie déterminantale de la fonction
d'essai, dans notre cas le déterminant Hartree-Fock. En localisant les
orbitales de ce déterminant, et en négligeant des petits coefficients des
orbitales moléculaires, les n![]() uds de la fonctoin d'onde seront alors
legèrement déplacés. Il y aura, par conséquent, concurrence entre
la bonne méthode (DMC) censée produire une énergie exacte à
partir d'une fonction d'essai approximative, et l'erreur des n
uds de la fonctoin d'onde seront alors
legèrement déplacés. Il y aura, par conséquent, concurrence entre
la bonne méthode (DMC) censée produire une énergie exacte à
partir d'une fonction d'essai approximative, et l'erreur des n![]() uds
fixés par cette fonction d'essai.
uds
fixés par cette fonction d'essai.
Dans un article recent[#!Grossman!#] J. Grossman a montré que cette erreur
des n![]() uds fixés est responsable d'erreurs sur les énergies de
formations calculées par DMC au même ordre de grandeur que celles des
calculs de chimie quantique traditionnelle, même si la méthode est
censée d'attendre une précision arbitraire, limitée uniquement par le
temps de calcul et la loi des grands nombres qui implique que l'erreur
statistique diminue comme l'inverse de la racine carrée du nombre des
tirages indépendants.
uds fixés est responsable d'erreurs sur les énergies de
formations calculées par DMC au même ordre de grandeur que celles des
calculs de chimie quantique traditionnelle, même si la méthode est
censée d'attendre une précision arbitraire, limitée uniquement par le
temps de calcul et la loi des grands nombres qui implique que l'erreur
statistique diminue comme l'inverse de la racine carrée du nombre des
tirages indépendants.