La description des surfaces ioniques

Cette approche a été proposé initialement par M. Causà à Turin[#!Ricca!#] et a été reprise et développée dans la suite. Une première implémentation, basée sur une version expérimentale de CRYSTAL92, a disparu depuis les travaux communs en 1995 et la publication [5]. Le système de programmes pour les calculs en orbitales localisées, dévéloppé depuis 1996, fournissait une bonne base de départ pour une implémentation plus homogène et moins dépendante du programme CRYSTAL. Elle inclue les multipôles dans la partie mono-électronique de l'opérateur de Fock et l'optimisation des multipôles en résolvant un système linéaire de dimension finie, parfaitement détachable du calcul quantique et ne nécessitant donc pas une structure périodique. Seul le potentiel électrostatique est calculé par un programme adapté aux systèmes périodiques.

Les limites du modèle choisi sont claires : la première est que les multipôles obtenus ne décrivent pas le potentiel en dehors de la région où le potentiel est calculé. La seconde limite est qu'il est impossible de reproduire le potentiel électrostatique dans les régions où la densité électronique de la surface est significative, puisque les multipôles sont inadéquats pour décrire un potentiel avec pénétration. Il est donc indispensable d'échantilloner la région complète de l'adsorption envisagée, à l'exception de sphères (par exemple rayons van der Waals) autour des atomes de la surface. Ceci exclut par exemple une description de la formation d'une liaison principalement covalente sur la surface. L'utilisation des fonctions diffuses dans la base de l'agrégat requiert également une attention particulière afin d'empécher les électrons de quitter l'agrégat. La prise en compte de la corrélation électronique demande d'ailleurs d'ajouter à la base optimisée pour des calculs Hartree-Fock des fonctions de corrélation relativement compactes, puisqu'une densité électronique corrélée est habituellement un peu plus compacte que la densité Hartree-Fock.

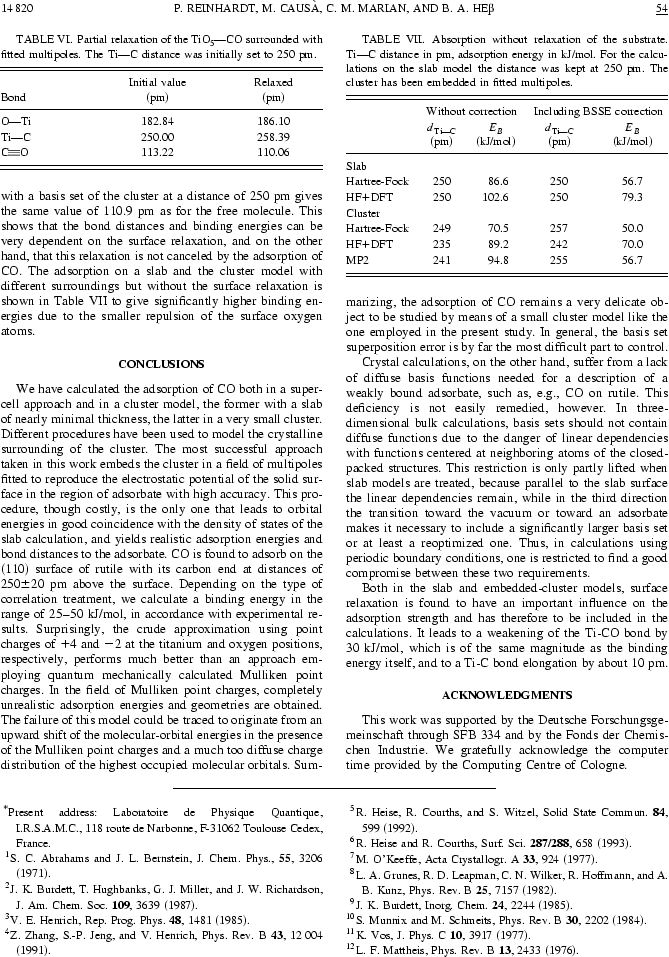
Nous reproduisons ici une figure de la publication [5], dont nous donnons la copie intégrale à la fin de ce chapitre, pour montrer ce que l'on peut obtenir par cette approche de multipôles déterminés d'une façon autocohérente à partir d'un calcul sur un système périodique.

**Figure 22:** Coincidence entre la densité d'états de la surface et sa modélisation par un agrégat TiO $_5^{6-}$ entouré de multipôles pour décrire l'adsorption de CO sur la surface (110) du rutile. La partie noire de la densité d'états est la projection sur les molécules de CO adsorbées sur la surface, tandis que la partie blanche est la projection sur les atomes de la surface, pris dans l'agrégat TiO $_5^{6-}$ .
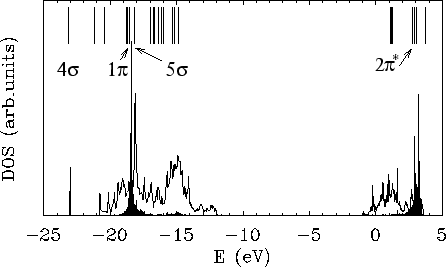
$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =7 true cm \epsffile {TiO2COdos.eps}\hfill}\end{displaymath} \end{figure}$

Les énergies des orbitales moléculaires de l'agrégat (et d'une molécule adsorbée) sont très sensibles à l'environnement électrostatique, comme le sont les énergies des orbitales de c $\oe$ ur en spectroscopie des surfaces. En visant de faire coïncider la densité d'états du calcul périodique avec les emplacements énergétiques des orbitales de l'agrégat nous avons un indice sur la qualité de l'extractions de multipôles. Cette coïncidence en valeurs absolues était beaucoup moins importante dans le cas de CuF

, puisque dans un solide tridimensionnel un entourage grossier conduit à un déplacement global de tout le spectre des énergies orbitalaires. Sur une surface, par contre, l'échelle des énergies est fixée par la limite de grandes distances; la coïncidence des énergies du calcul périodique via la densité d'états et du calcul modèle utilisant un agrégat avec entourage devient essentielle.

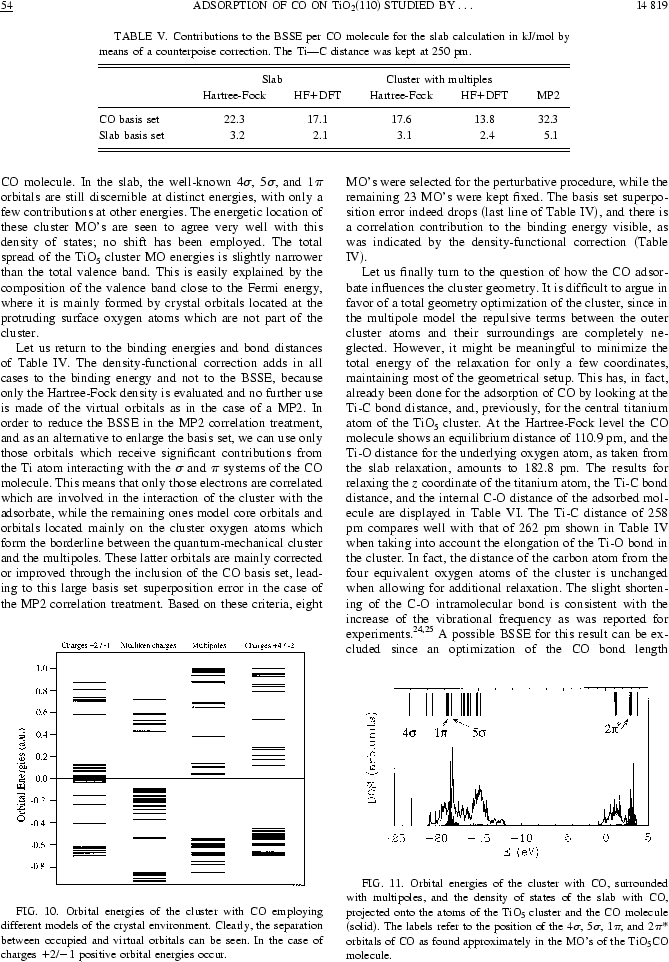
L'exemple de TiO

a montré qu'il est impossible de reproduire le spectre à l'aide des seules charges ponctuelles, ce qui oblige à considérer des multipôles d'ordre supérieur. La procédure mise en $\oe$ uvre comprend plusieurs étapes :

Les étapes 3 à 7 exigent des implémentations nouvelles, capables de gérer des multipôles au delà des simples charges. Pour l'instant les charges, les dipôles et les quadrupôles sont utilisables, mais la généralisation aux multipôles d'ordre plus élevé n'est pas difficile.

L'étape 3 passe par la différence entre le potentiel électrostatique de la surface idéale et le potentiel provoqué par les atomes de l'agrégat quantique, coupé du solide. En pratique on extrait les éléments de la matrice de la densité électronique du système périodique correspondants aux atomes de l'agrégat,[2]Le nombre d'électrons dans cette partie de la matrice densité périodique n'est qu'approximativement celui de l'agrégat considéré. leur potentiel étant calculé séparément. Les multipôles de départ devront correspondre grossièrement à cette différence des potentiels. Dans les étapes 4 à 7 une autre base d'orbitales atomiques peut être employée, et les multipôles sont corrigés pour correspondre au nombre d'électrons de l'agrégat et à une repartition des électrons légèrement différente. Les itérations de l'optimisation des multipôles n'ont pas toujours un point de convergence correspondant à une situation physique -- nous devrons plutôt utiliser la coïncidence énergétique comme critère pour décider de la fin de l'optimisation.

Comme toujours, le diable est caché dans les détails. L'optimisation des multipôles est une procédure extrêmement délicate, à cause des dépendances linéaires entre multipôles d'ordres différents. Le choix des points, dans lesquels le potentiel est déterminé, le nombre de multipôles à considérer, tout cela demande des études préalables et beaucoup d'expérience. Une fois maîtrisée, la méthode d'entourage par des multipôles devrait concurrencer d'autres approches utilisés.

J'ai alors (re-)implémenté à Paris la procédure dans le logiciel expérimental pour obtenir une plus grande flexibilité et pour également profiter des développements concernant la corrélation électronique. Ce travail est en cours de développement. Nous en donnons quelques résultats préliminaires, sur l'exemple de la surface (001) de MgO.

Ce cristal très ionique de structure NaCl ne montre pas de relaxation des atomes de la surface. Un modèle simple est constitué par un agrégat MgO $_5^{8-}$ entouré de charges de symétrie C $_{4v}$ . Un calcul périodique de la surface, en utilisant un film mince de 12 couches ioniques est d'abord effectué. On trouve avec 1690 positions, réduites à 272 multipôles irréductibles grâce à la symétrie, un ensemble neutre autour de l'agrégat MgO $_5^{8-}$ en prenant des charges $\pm$ 2 sur chaque centre ionique.

Le premier ajustement des multipôles est fait avec environ 800 points dans la région de l'agrégat et en imposant une charge totale de +8 pour l'ensemble des multipôles. Les charges sont optimisées une par une en minimisant la différence entre le potentiel créé par les multipôles et celui de la surface périodique sans les atomes de l'agrégat. Une fois chaque charge de l'entourage corrigée, la procédure peut être relancée, et après cinq cycles d'optimisation les charges et le potentiel se stabilisent.

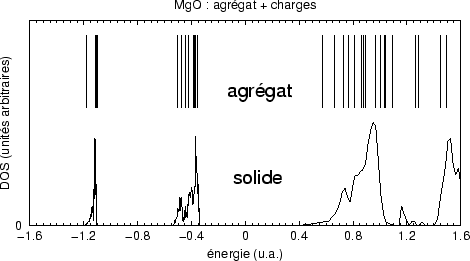
A ce stade nous utilisons le réseau de points de potentiel au dessus de la surface pour lancer les optimisations autocohérentes. Deux itérations permettent d'obtenir un bon ensemble, avec la coïncidence recherchée :

**Figure 23:** Densité d'états et énergies des orbitales de l'agrégat, entouré de charges adaptées. Les même bases atomiques ont été utilisées pour les deux calculs.
$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =6 true cm \epsffile {FitMgO.eps}\hfill}\end{displaymath} \end{figure}$

**Figure 24:** Valeurs absolues des charges (irréductibles) autour de l'agrégat de MgO $_5^{8-}$ , indiquant que la portée de la zone quantique se limite grosso modo aux 25 premières positions.
$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =4 true cm \epsffile {chargesMgO.eps}\hfill}\end{displaymath} \end{figure}$

Dans le cas du cristal de MgO nous n'avons pas trouvé de point stable en incluant les dipôles et les quadrupôles. Le cristal ionique, d'une structure compacte, apparaît être bien décrit par des ions sphériques et de sorte que les multipôles d'ordre supérieur n'améliorent que localement la qualité du potentiel, d'autant que les contributions entre des multipôles d'ordres différents se compensent en partie. Dans le cas de TiO

la structure plus ouverte et la coodination des ions plus variée rend nécessaire d'aller au delà de simples charges.

Les valeurs des charges dans MgO après l'adaptation ne sont pas très différentes des valeurs intiales de $\pm$ 2 (Fig. 24). L'analyse de population de Mulliken donne dans les deux cas, calcul périodique et agrégat, des atomes parfaitement ioniques :

$\begin{displaymath} % latex2html id marker 3659\begin{minipage}{10 true cm} \b... ...t.) & 9.981 & 10.012 \\ \end{tabular}\end{table}\end{minipage}\end{displaymath}$

Une fois l'entourage déterminé, l'étude de l'adsorption de CO (avec prise en compte de la corrélation) peut être effectuée comme nous l'avons montré dans la publication [5]. Le même environnement peut être ensuite utilisé pour des calculs avec des bases différentes.

A ce stade actuel de développement la nouvelle version du logiciel donne de bons résultats. Il faut souligner que l'ajustement des multipôles est nécessaire pour tenir compte :

Une alternative à l'ajustement de multipôles aux longues distances peut être d'évaluer le potentiel d'un ensemble de multipôles infini par la méthode d'Ewald[#!Ewald!#,#!Mertins!#] et d'ajouter une correction locale autour de l'agrégat fini pour tenir compte de la pénétration.

Avant de programmer la sommation d'Ewald, il est possible d'envisager d'autres applications telles que les surfaces d'Al

, la description de la relaxation en incluant la corrélation électronique au delà de l'approximation Hartree-Fock ou des études d'autre surfaces très ioniques, difficilement traitables par les méthodes ``à la mode'' de développement d'orbitales sur des ondes planes.

Une autre suite sera l'application à des surfaces de la glace comme modèle d'une comète et l'adsorption de molécules simples par son voyage dans l'espace. Dans ce cas il ne s'agit plus d'un cristal ionique, mais d'un ensemble de dipôles moléculaires, où l'utilisation des multipôles au delà de simples charges devrait jouer un rôle plus important. Dans le même domaine astrophysique la formation des météorites ou les questions d'exobiogologie (formation de premières molécules de la vie) peuvent être abordées.

$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page1.eps}\hfill}\end{displaymath} \end{figure}$

$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page2.eps}\hfill}\end{displaymath} \end{figure}$

$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page3.eps}\hfill}\end{displaymath} \end{figure}$

$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page4.eps}\hfill}\end{displaymath} \end{figure}$

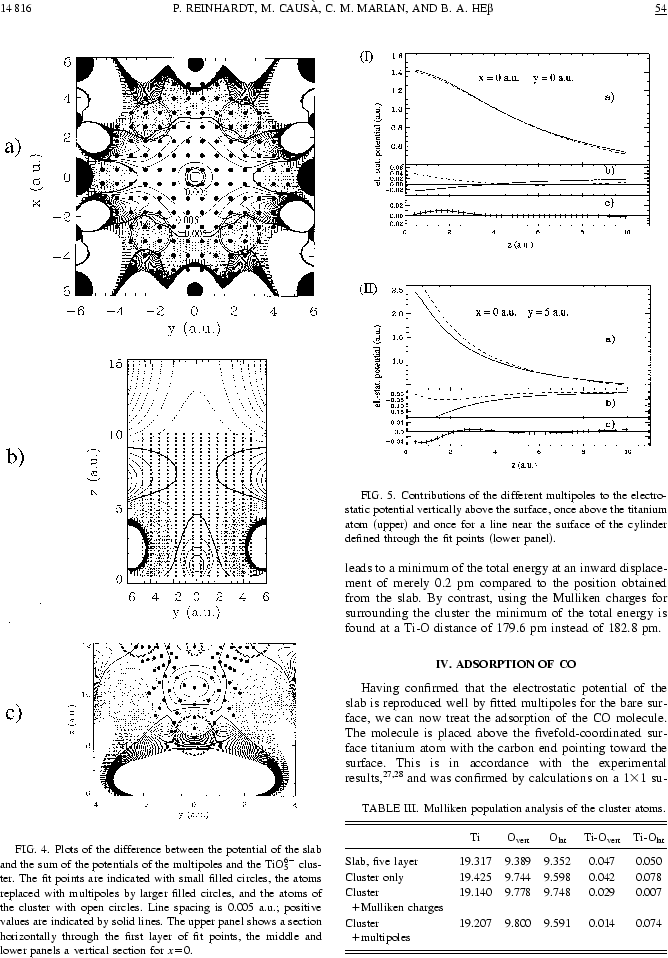
$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page5.eps}\hfill}\end{displaymath} \end{figure}$

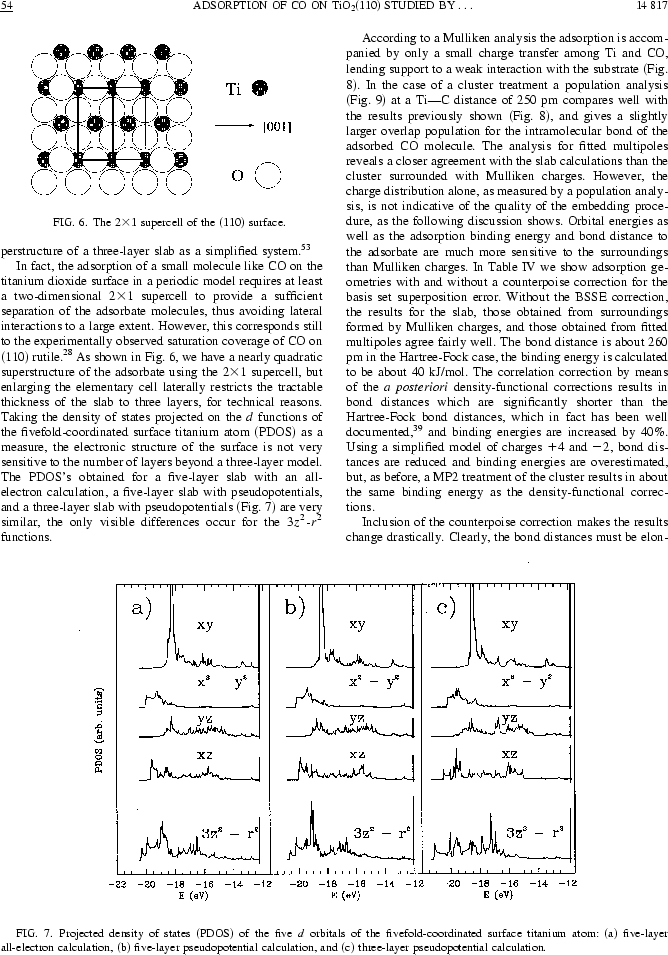
$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page6.eps}\hfill}\end{displaymath} \end{figure}$

$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page7.eps}\hfill}\end{displaymath} \end{figure}$

$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page8.eps}\hfill}\end{displaymath} \end{figure}$

$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page9.eps}\hfill}\end{displaymath} \end{figure}$

$\begin{figure} \begin{displaymath}\vbox{\hfil\hskip -1 true cm\epsfysize =23 true cm \epsffile{TiO2_page10.eps}\hfill}\end{displaymath} \end{figure}$