Les surfaces polaires

Une autre application des entourages, également utilisée dans la littérature, concerne les problèmes de surfaces, de relaxation, d'adsorptions et de réactions induites par des défauts comme des marches, des lacunes ou des adatomes. Là encore, pseudopotentiels et charges ponctuelles sont considérées comme des outils de travail habituels.[#!ClusterModel!#]

Intéressons-nous d'abord à l'exemple très simple d'une surface polaire. Dans ces surfaces les ions positifs et négatifs ne sont pas dans une seule couche neutre, mais forment chacun une couche bidimensionnelle. A l'intérieur du solide, chaque couche est stabilisée par les couches voisines. Or la dernière couche, celle de surface, n'a pas de couches voisines symétriques, et va donc être attirée vers l'intérieur du crystal. La conséquence immédiate est la création d'un dipôle perpendiculaire à la surface.

Au delà de cette vision simple, de nombreux auteurs ont discuté depuis longtemps de savoir si ces surfaces peuvent avoir un moment dipolaire ou pas. Déjà Pierre Curie s'était intéressé à ces problématiques, en étudiant la pyroélectricité, c'est à dire des charges de surfaces induites par la dilatation d'un crystal en fonction de la température. Un argument relativement simple, mis en avant par les travaux de Tasker,[#!Tasker!#] est qu'une surface polaire de taille infinie ne peut avoir un moment non nul par maille élémentaire, car la somme sur tout les dipôles de cette surface -- et un dipôle macroscopique -- serait infinie. Donc les moments existants seraient dûs aux limites de taille finie. Or, comme les calculs sur les systèmes étendus fournissent l'énergie et les moments électrostatiques par cellule, cette limite macroscopique n'entre pas explicitement dans le calcul.

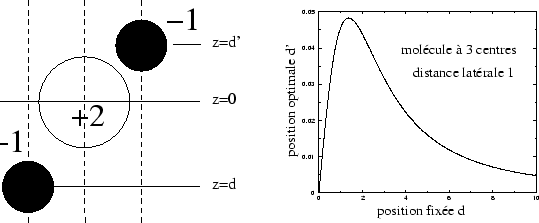
Le modèle que nous allons étudier est constitué de trois charges, une positive (+2) et deux négatives ($-1$). En fixant la position de deux d'entre elles, la question est de savoir où va se mettre la troisième, si sa position reste libre en $z$, mais fixée en $x$ et $y$. Les limites sont claires, puisque pour $z=0$ et $z=\infty$ de la charge négative fixée, la charge négative libre va se retrouver à $z=0$. Entre ces deux extrêmes c'est la position indiquée qui est adoptée, induisant immédiatement un dipôle avec une composante en $z$.

Figure 21: Modèle à trois charges et position $d'$ optimale de la charge libre, en fonction de la position $d$ de la charge fixée.

Le modèle peut être étendu à des chaînes uni-dimensionnelles ou des grilles bidimensionnelles, qualitativement avec le même résultat, c'est à dire qu'il n'y a pas d'effet répulsif, empêchant l'existence d'un moment dipolaire perpendiculaire à la surface. En tous cas, la contribution de la sommation infinie des dipôles ne joue aucun rôle sur l'énergie totale de la surface.

Avec un modèle hémisphérique et simplifié du solide, j'ai retrouvé les mêmes résultats. Par conséquent, il est parfaitement possible de minimiser l'énergie totale sans introduire une contrainte sur le moment dipolaire.

L'expérimentation numérique avec des modèles sémi-empiriques et ab-initio (Réf. Massanidis et publication [13]) montre que la corrélation électronique contribue significativement à la relaxation des premières couches d'atomes, même pour un cristal aussi simple et ionique que Al$_2$O$_3$. Obtenir des valeurs fiables reste un défi théorique, d'autant plus que les expérimentateurs ont difficilement accès à ces informations par diffraction d'électrons (XPD ou LEED) ou par microscopie à effet tunnel (STM).