Ce chapitre n'est pas seulement consacré à la recherche et la mise en place d'une procédure de perturbation performante, mais également à discuter les limites et les caractéristiques des différents types de localisation. Puisque ces calculs sur un solide tridimensionnel sont relativement lourds, comme nous l'avons montré avec CEPA-0, les anneaux ou même les dimères nous ont semblé des systèmes accessibles et réprésentatifs.
Les dimères en interaction posent un défi supplémentaire : les interactions entre molécules à couches fermées, sans liaison chimique, sont en général faibles, proche de la précision numérique du calcul. L'utilisation des méthodes de type ``supermolécule'', qui consiste à calculer l'énergie d'interaction en soustraiant de l'énergie totale du dimère celles des monomères, nécessite de tenir compte en plus de la correction de l'erreur de superposition de base (BSSE).
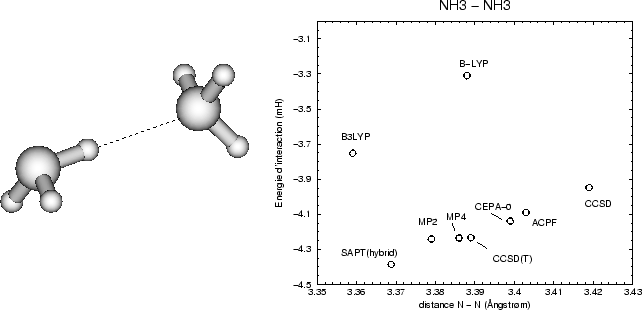
Nous présentons alors l'exemple de ce chapitre : le dimère de NH![]() dans des bases optimisées pour des calculs d'interactions
intermoléculaires[#!Voisin!#], utilisées dans l'article [16].
La figure donne une idée générale de la performance des différentes
méthodes de calcul de l'énergie d'interaction, montrant une précision de
dans des bases optimisées pour des calculs d'interactions
intermoléculaires[#!Voisin!#], utilisées dans l'article [16].
La figure donne une idée générale de la performance des différentes
méthodes de calcul de l'énergie d'interaction, montrant une précision de
![]() 5
5![]() pm pour la longueur de liaison et de
pm pour la longueur de liaison et de ![]() 0.2
0.2![]() mH (env. 0.15
mH (env. 0.15![]() kcal/mol) à envisager.
kcal/mol) à envisager.
 |
Avant de montrer le calcul de l'énergie d'interaction nous introduisons les différentes variantes de la perturbation Epstein-Nesbet, en ne partant plus des méthodes CEPA comme il l'était indiqué au debut de ce chapitre, mais en les construisant successivement à partir de la théorie des perturbations dans sa forme diagrammatique.
L'hamiltonien H est séparé en une partie H![]() , dont la
solution est connue, et la perturbation V. Le choix
Møller-Plesset[#!MollerPlesset!#], le plus simple dans le contexte ici,
est de prendre
, dont la
solution est connue, et la perturbation V. Le choix
Møller-Plesset[#!MollerPlesset!#], le plus simple dans le contexte ici,
est de prendre
![]() , l'opérateur mono-électronique de la solution
Hartree-Fock connue. Avec cet opérateur l'énergie totale en premier ordre
est l'énergie Hartree-Fock, et la corrélation en deuxième ordre est
représentée par deux diagrammes génériques,
, l'opérateur mono-électronique de la solution
Hartree-Fock connue. Avec cet opérateur l'énergie totale en premier ordre
est l'énergie Hartree-Fock, et la corrélation en deuxième ordre est
représentée par deux diagrammes génériques,
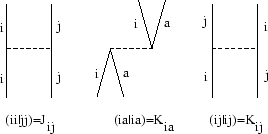
à évaluer selon les règles de Goldstone.[#!Goldstone!#,#!Brandow!#] Pour des systèmes à couches fermées la sommation sur des différentes combinaisons des spins des orbitales i, j, a et b peut être executée, donnant ainsi une formule simple :
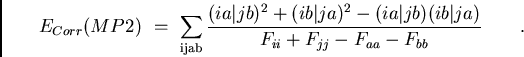 |
(15) |
En orbitales canoniques les diagrammes ne sont constitués que des
interactions biélectroniques et d'indices uniques, puisque les interactions
monoélectroniques diagonales par l'opérateur de Fock sont incluses dans
H![]() et celles qui peuvent
changer un indice sur une ligne de propagation sont strictement nuls. En
orbitales localisées ce deuxième point n'est plus valable : il peut bien y
avoir des changements d'indices sur les lignes de propagation via des
interactions par des éléments non-diagonaux de F. Ceci indique un
des problèmes de la théorie de perturbations en orbitales localisées :
les résultats sont dépendants de la localisation
choisie.[2]Il est possible d'inverser cette logique en
cherchant une
procédure produisant des orbitales qui donneraient les mêmes résultats
qu'un calcul CCSD(T) par exemple, mais moins coûteux. Les orbitales
Brueckner ou les Pair Natural Orbitals (PNO) ont été conçues dans cet
esprit.
Deux solutions sont à envisager.
et celles qui peuvent
changer un indice sur une ligne de propagation sont strictement nuls. En
orbitales localisées ce deuxième point n'est plus valable : il peut bien y
avoir des changements d'indices sur les lignes de propagation via des
interactions par des éléments non-diagonaux de F. Ceci indique un
des problèmes de la théorie de perturbations en orbitales localisées :
les résultats sont dépendants de la localisation
choisie.[2]Il est possible d'inverser cette logique en
cherchant une
procédure produisant des orbitales qui donneraient les mêmes résultats
qu'un calcul CCSD(T) par exemple, mais moins coûteux. Les orbitales
Brueckner ou les Pair Natural Orbitals (PNO) ont été conçues dans cet
esprit.
Deux solutions sont à envisager.
Soit on garde tout les éléments de F dans H![]() , alors le
dénominateur
, alors le
dénominateur
![]() n'est plus
composé de simples différences d'énergies d'orbitales et le résultat
est une solution autocohérente d'un système d'équations linéaires --
il s'agit du même système d'équations que celui donné en Equation
11, avec la différence que l'on utilise les éléments
de la matrice F au lieu des
n'est plus
composé de simples différences d'énergies d'orbitales et le résultat
est une solution autocohérente d'un système d'équations linéaires --
il s'agit du même système d'équations que celui donné en Equation
11, avec la différence que l'on utilise les éléments
de la matrice F au lieu des ![]() , ne couplant ainsi que des
déterminants avec une seule différence d'occupation des orbitales. Cette
variante est utilisée relativement souvent puisque les résultats sont
invariants par rapport aux rotations d'orbitales par exemple par
localisations. Au delà de MP2 S. Saebo et P. Pulay ont montré[#!PulayII!#]
comment on peut écrire les équations de MP4 (sans triple excitations)
d'une façon invariante en orbitales localisées.
, ne couplant ainsi que des
déterminants avec une seule différence d'occupation des orbitales. Cette
variante est utilisée relativement souvent puisque les résultats sont
invariants par rapport aux rotations d'orbitales par exemple par
localisations. Au delà de MP2 S. Saebo et P. Pulay ont montré[#!PulayII!#]
comment on peut écrire les équations de MP4 (sans triple excitations)
d'une façon invariante en orbitales localisées.
Comme alternative nous pouvons exclure les éléments non-diagonaux de H![]() en les rajoutant à la perturbation V -- une deuxième
série de diagrammes est à évaluer, cette fois-ci impliquant F :
en les rajoutant à la perturbation V -- une deuxième
série de diagrammes est à évaluer, cette fois-ci impliquant F :
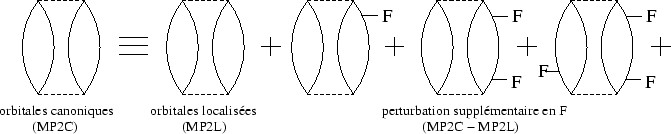 |
En ne gardant que le premier diagramme du coté droit de ``l'équation''
dans figure 9, une grande partie de l'énergie de corrélation est
négligée. Mais le défaut plus sevère est l'introduction d'une
dépendance de la localisation utilisée. Nous avons essayé de réduire
cette dépendance par des sommations ordre par ordre des éléments
non-diagonaux de F, ce qui se montre relativement lourd, comme tout
traitement de la perturbation ordre par ordre. Chaque augmentation de l'ordre
introduit grosso modo un facteur de ![]() (nombre de fonctions de base) dans la
calcul par la sommation d'un indice supplémentaire;
(nombre de fonctions de base) dans la
calcul par la sommation d'un indice supplémentaire; ![]() pour MP2,
pour MP2, ![]() pour MP3 et
pour MP3 et ![]() inévitablement pour MP4, également à cause des triples
excitations. Une solution itérative ramène le coût de MP4 à
inévitablement pour MP4, également à cause des triples
excitations. Une solution itérative ramène le coût de MP4 à ![]() , si
l'on ne tient pas compte des états tri-excités.
Il est possible d'effectuer des sommations infinies partielles ne
considérant que les diagrammes de perturbation les plus importants,
ce qui stabilise les résultats sans augmenter significativement le coût
global du calcul. Les publications [8], [9] et
[11] proposent quelques possibilités.
, si
l'on ne tient pas compte des états tri-excités.
Il est possible d'effectuer des sommations infinies partielles ne
considérant que les diagrammes de perturbation les plus importants,
ce qui stabilise les résultats sans augmenter significativement le coût
global du calcul. Les publications [8], [9] et
[11] proposent quelques possibilités.
La sommation infinie et complète conduit au système d'équations
linéaires mentionnés, analogue du CEPA, qui est la sommation infinie de
tout les diagrammes de perturbation liés impliquant des déterminants
diexcités (DMBPT-![]() ).
).
Gardant ceci en mémoire, nous pouvons également ne sommer que certaines interactions bi-électroniques vers infini, en utilisant une partition différente de l'hamiltonien. En restant au deuxième ordre de perturbation la décomposition Epstein-Nesbet[#!EpsteinNesbet!#] de l'hamiltonien exact
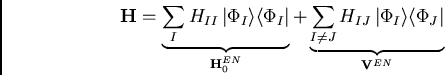 |
(16) |
 |
Par rapport à la perturbation Møller-Plesset, on s'aperçoit cependant
des
inconvénients de la formulation Epstein-Nesbet : il faut un développement
en déterminants au lieu d'un développement en indices d'orbitales. Pour
une diexcitation
![]() il est nécessaire de respecter les six
combinaisons de spins individuellement, ce qui introduit une dépendance
supplémentaire, celle des couplages de spins. Néanmoins il est
possible (Référence Silver et publication
[7]) de réduire la dépendance des couplages de spin à
une combinaison unique.
il est nécessaire de respecter les six
combinaisons de spins individuellement, ce qui introduit une dépendance
supplémentaire, celle des couplages de spins. Néanmoins il est
possible (Référence Silver et publication
[7]) de réduire la dépendance des couplages de spin à
une combinaison unique.
La sommation des diagrammes d'interaction biélectroniques en orbitales
localisées sera appellée alors dans la suite EN2L. L'évaluation exacte de la
série infinie de l'opérateur de Fock en perturbation
Epstein-Nesbet (EN2L) pourrait se faire en remplaçant la diagonale H![]() par H
par H![]() dans le système des équations
linéaires du MP2. L'effort calculatoire supplémentaire est presque
négligeable.
dans le système des équations
linéaires du MP2. L'effort calculatoire supplémentaire est presque
négligeable.
Avant de tester les différentes possibilités, il faut être conscient qu'il n'est pas nécessairement souhaitable de reproduire en orbitales localisées les résultats que l'on obtient en orbitales canoniques. Deux particularités importantes de la perturbation Epstein-Nesbet ne doivent pas être oubliées. Les corrections Epstein-Nesbet changent les dénominateurs de chaque contribution Møller-Plesset par les interaction supplémentaires J et K.
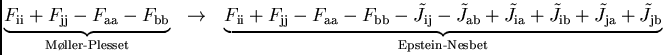 |
(17) |
Or, en orbitales canoniques, J et K
diminuent avec la délocalisation sur ![]() atomes comme 1/
atomes comme 1/![]() . Par
conséquent, dans la limite d'un système infini, la sommation infinie de
diagrammes devient nulle et on se retrouve encore avec le résultat MP2. En
prenant par contre des orbitales localisées les J et K, couplant
trous et particules spatialement proches, restent grandes, indépendamment de
la taille totale du système. Dans ce cas la perturbation Epstein-Nesbet
reste différente de la perturbation Møller-Plesset.
. Par
conséquent, dans la limite d'un système infini, la sommation infinie de
diagrammes devient nulle et on se retrouve encore avec le résultat MP2. En
prenant par contre des orbitales localisées les J et K, couplant
trous et particules spatialement proches, restent grandes, indépendamment de
la taille totale du système. Dans ce cas la perturbation Epstein-Nesbet
reste différente de la perturbation Møller-Plesset.
La deuxième particularité concerne les interaction intermoléculaires,
mais vient d'un argument similaire.[#!Fernand!#] L'interaction Coulombienne
J des trous et particules situés sur deux fragments séparés par
une distance ![]() est proportionnelle à 1/
est proportionnelle à 1/![]() . Une orbitale
. Une orbitale ![]() complètement délocalisée sur deux centres provoquera donc une interaction
artificielle (nous négligeons les densités de recouvrement en
mettant
complètement délocalisée sur deux centres provoquera donc une interaction
artificielle (nous négligeons les densités de recouvrement en
mettant
![]() ) :
) :
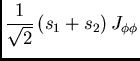 |
(18) |
En orbitales localisées, sans occupation des orbitales sur des sites voisins, cette interaction artificielle n'existe pas. En orbitales parfaitement localisées (molécules sans interactions), la perturbation Epstein-Nesbet est alors size-consistent. Mais en réalité les orbitales débordent toujours un peu et donc, contrairement à la décomposition Møller-Plesset, l'énergie de corrélation par atome dépend toujours (faiblement) de la taille du système.
Aux ``corrections'' de l'énergie MP2 par des diagrammes d'ordres
supérieurs peuvent se rajouter celle correspondant à toute la classe des
diagrammes EPV des habillages du chapitre précédent : il suffit de
reconnaître que les équations Epstein-Nesbet sont données par la
diagonale de la matrice CEPA de l'équation 11. En
utilisant les expressions des tableaux I et II,
nous ajoutons successivement les EPV, ou des estimations moyennes par ACPF ou
AQCC.[2]Une approche complémentaire, passant par des
rotations 2![]() 2 de petites matrices d'IC habillées a été donnée
par M.-B. Lepetit et J.-P. Malrieu dans Réfs. MarieI et
etables. Ce faisant, les éléments non-diagonaux de
l'opérateur de Fock ne sont pas introduits et pourraient être ajoutés en
cherchant les coefficients de l'expression de l'énergie de corrélation.
Ceci consiste à remplacer en remplaçant les éléments non-diagonaux
2 de petites matrices d'IC habillées a été donnée
par M.-B. Lepetit et J.-P. Malrieu dans Réfs. MarieI et
etables. Ce faisant, les éléments non-diagonaux de
l'opérateur de Fock ne sont pas introduits et pourraient être ajoutés en
cherchant les coefficients de l'expression de l'énergie de corrélation.
Ceci consiste à remplacer en remplaçant les éléments non-diagonaux
![]() par
par
![]() dans
équation 11.
dans
équation 11.
Une estimation plus simple de l'effet des éléments non-diagonaux de F est donnée par la différence entre l'énergie de corrélation MP2 en orbitales canoniques (MP2C) et celle en orbitales localisées (MP2L), c'est à dire la sommation infinie à droite de la figure 9. Même si on ne regarde alors qu'une petite partie de l'action de l'opérateur de Fock sur la série construite par la sommation infinie Epstein-Nesbet, puis les contributions diverses des EPV, cette approximation semble déjà utile. En effet, les sommations des EPV diminuent les surestimations par la perturbation Epstein-Nesbet d'un coté; de l'autre coté, l'impact des éléments non-diagonaux de F peut être modéré en ne diagonalisant que partiellement l'opérateur de Fock, sans délocaliser les orbitales moléculaires. Par conséquent les éléments de F les plus grands, couplant trous et particules proches, disparaissent.
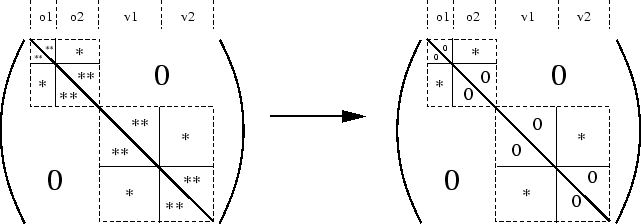 |
Pour l'étude des interactions inter-moléculaires dans un dimère il est intéressant d'avoir des orbitales localisées sur les monomères, alors que la localisation à l'intérieur d'une molécule est moins intéressante. J'ai donc proposé d'attribuer les orbitales moléculaires, occupées et virtuelles, aux deux monomères et de ne diagonaliser l'opérateur de Fock que sur les monomères.
Les deux molécules NH![]() de l'exemple sont inéquivalentes, ce qui fait
que déjà les orbitales canoniques sont plus ou moins localisées sur l'un
ou l'autre des deux monomères. Mais on peut utiliser évidemment toutes les
stratégies disponibles pour localiser davantage les orbitales.
Entre deux jeux d'orbitales
de l'exemple sont inéquivalentes, ce qui fait
que déjà les orbitales canoniques sont plus ou moins localisées sur l'un
ou l'autre des deux monomères. Mais on peut utiliser évidemment toutes les
stratégies disponibles pour localiser davantage les orbitales.
Entre deux jeux d'orbitales ![]() and
and ![]() correspondant au même
déterminant de Slater, résultant de deux procédures de localisation
différentes, il y a toujours une transformation orthogonale T donnée
par
correspondant au même
déterminant de Slater, résultant de deux procédures de localisation
différentes, il y a toujours une transformation orthogonale T donnée
par
![]() . Et, puisque n'importe quelle matrice
orthogonale peut être diagonalisée dans l'éspace complexe par une
transformation unitaire U (
. Et, puisque n'importe quelle matrice
orthogonale peut être diagonalisée dans l'éspace complexe par une
transformation unitaire U (
![]() )
)
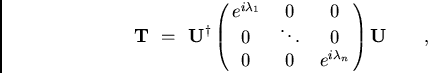 |
(19) |
 |
En identifiant les orbitales entre ![]() (i.e.
(i.e.
![]() ) et
) et ![]() (i.e.
(i.e. ![]() ) nous avons alors un chemin
continu entre les deux localisations, sans passer par une délocalisation
accidentelle par croisement d'orbitales le long de ce chemin. Cet outil permet
de suivre l'énergie de corrélation en fonction du type de localisation des
orbitales. Pour illustration, les orbitales Pipek-Mezey et les orbitales Boys
(occupées et virtuelles), sont construites à partir des orbitales
canoniques du dimère NH
) nous avons alors un chemin
continu entre les deux localisations, sans passer par une délocalisation
accidentelle par croisement d'orbitales le long de ce chemin. Cet outil permet
de suivre l'énergie de corrélation en fonction du type de localisation des
orbitales. Pour illustration, les orbitales Pipek-Mezey et les orbitales Boys
(occupées et virtuelles), sont construites à partir des orbitales
canoniques du dimère NH![]() NH
NH![]() . La procédure de diagonalisation
de F sur les monomères est appliquée pour chaque
. La procédure de diagonalisation
de F sur les monomères est appliquée pour chaque ![]() après
l'opération de localisation avec T(
après
l'opération de localisation avec T(![]() ). Dans ce cas T(0)
transforme les orbitales canoniques en orbitales Pipek-Mezey et par T(1)
nous obtenons les orbitales de la localisation de Boys.
). Dans ce cas T(0)
transforme les orbitales canoniques en orbitales Pipek-Mezey et par T(1)
nous obtenons les orbitales de la localisation de Boys.
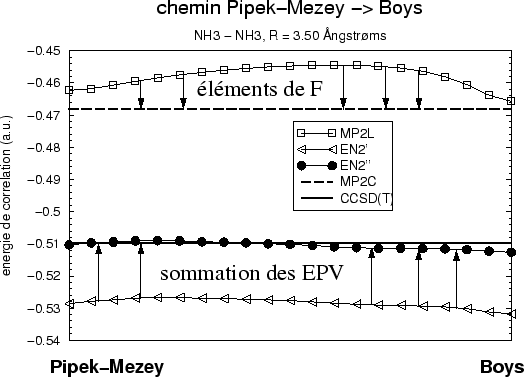
De la multitude de variantes possibles selon les habillages différents nous
ne montrons que l'inclusion de l'ensemble complet des EPV (habillage
autocohérente du (SC)![]() CI de tableau I) dans figure
12.
CI de tableau I) dans figure
12.
Il faudrait peut-être préciser que l'autocohérence de l'habillage ne
nécessite pas d'itération par diagonalisation de la matrice CEPA (éq.
11), mais seulement la réintroduction des coefficients
c![]() dans l'habillage. Le processus reste donc toujours très peu coûteux,
d'autant plus que le calcul de l'énergie MP2C (MP2 en orbitales canoniques)
peut se faire au même coût en utilisant des orbitales canoniques
directement. La figure montre bien que l'énergie de corrélation obtenue
n'est pas que le résultat d'une compensation entre sommations différentes :
la sommation sur F a une structure bien différente de celle de la
sommation des EPV. La présence des deux permet la comparaison directe avec
les résultats CCSD(T); les autres habillages par des sous-ensembles d'EPV
donnent des résultats intermédiaires.
dans l'habillage. Le processus reste donc toujours très peu coûteux,
d'autant plus que le calcul de l'énergie MP2C (MP2 en orbitales canoniques)
peut se faire au même coût en utilisant des orbitales canoniques
directement. La figure montre bien que l'énergie de corrélation obtenue
n'est pas que le résultat d'une compensation entre sommations différentes :
la sommation sur F a une structure bien différente de celle de la
sommation des EPV. La présence des deux permet la comparaison directe avec
les résultats CCSD(T); les autres habillages par des sous-ensembles d'EPV
donnent des résultats intermédiaires.
=1
= 1
Evitant les procédures a posteriori de localisation (Boys et Pipek-Mezey), nous proposons d'essayer la même stratégie avec des orbitales obtenues à partir de l'interaction de déterminants monoexcités, en partant des orbitales canoniques des monomères. L'opérateur de Fock est également diagonalisé sur les monomères, après avoir obtenu la solution Hartree-Fock du dimère.
En orbitales canoniques, malgré la délocalisation, la perurbation
Epstein-Nesbet donne sans habillage une bonne énergie de corrélation avec
une legère surestimation. Dans ce cas il n'y a pas de sommation via les
éléments non-diagonaux de F, mais il existe celle des EPV, d'où la
performance moins bonne d'ACPF et (SC)![]() .
.
En orbitales localisées, en incluant la série de F et des EPV, nous
obtenons en revanche à 0.5![]() % près l'énergie CCSD(T) par un calcul
de perturbation.
% près l'énergie CCSD(T) par un calcul
de perturbation.
Aprés avoir constaté la bonne performance de l'approximation proposée
pour le système NH![]() NH
NH![]() , un autre problème doit être résolu.
L'opérateur de Fock du dimère est diagonalisé dans l'espace des
monomères. Il convient donc, pour calculer l'énergie d'interaction,
d'utiliser des orbitales canoniques dans la base des monomères, c'est à
dire d'introduire l'erreur de superposition de bases (BSSE). Pour compenser
cette erreur, les calculs des monomères se font dans la base complète du
dimère. Mais, en diagonalisant l'opérateur de Fock nous délocalisons les
orbitales virtuelles sur l'ensemble des deux monomères, et les arguments
évoqués auparavant, concernant les intégrales J et K restent
parfaitement valables, même pour les orbitales virtuelles. Alors nous avons
proposé une procédure différente pour générer des orbitales de
chaque monomère : aux orbitales canoniques du monomère nous ajoutons la
base de l'autre monomère. L'IC des
monoexcitations relaxe ensuite les orbitales moléculaires dans la grande
base, en touchant le moins possible aux orbitales initiales. Ainsi les
orbitales virtuelles restent à leur place (dans l'espace) et conservent
leur énergie monoélectronique le plus possible. Ensuite on pourrait même
diagonaliser l'opérateur de Fock sur l'espace de orbitales occupées, sur
l'espace des orbitales virtuelles centrées sur la molécule, et sur
l'espace des orbitales vituelles centrées sur la base fantôme.
, un autre problème doit être résolu.
L'opérateur de Fock du dimère est diagonalisé dans l'espace des
monomères. Il convient donc, pour calculer l'énergie d'interaction,
d'utiliser des orbitales canoniques dans la base des monomères, c'est à
dire d'introduire l'erreur de superposition de bases (BSSE). Pour compenser
cette erreur, les calculs des monomères se font dans la base complète du
dimère. Mais, en diagonalisant l'opérateur de Fock nous délocalisons les
orbitales virtuelles sur l'ensemble des deux monomères, et les arguments
évoqués auparavant, concernant les intégrales J et K restent
parfaitement valables, même pour les orbitales virtuelles. Alors nous avons
proposé une procédure différente pour générer des orbitales de
chaque monomère : aux orbitales canoniques du monomère nous ajoutons la
base de l'autre monomère. L'IC des
monoexcitations relaxe ensuite les orbitales moléculaires dans la grande
base, en touchant le moins possible aux orbitales initiales. Ainsi les
orbitales virtuelles restent à leur place (dans l'espace) et conservent
leur énergie monoélectronique le plus possible. Ensuite on pourrait même
diagonaliser l'opérateur de Fock sur l'espace de orbitales occupées, sur
l'espace des orbitales virtuelles centrées sur la molécule, et sur
l'espace des orbitales vituelles centrées sur la base fantôme.
true cm
Ceci conduit à (tableau IV) un effet inattendu, mais
facilement explicable -- en ajoutant la base fantôme au monomère,
l'énergie de corrélation diminue en Epstein-Nesbet, et
également avec les habillages ACPF et (SC)![]() . Donc même en gardant le
plus possible l'équivalent des orbitales du dimère nous n'obtenons jamais
de correction BSSE dans la bonne direction, les valeurs dans la base du
dimère sont toujours moins importantes que dans la base des monomères.
Alors la notion du BSSE devient différente : la délocalisation sur l'autre
monomère, avec orbitales localisées ou canoniques, étant plus grand aux
courtes distances, introduit une correction opposée à celle des
autres méthodes de corrélation, pour lesquelles la règle générale
est valable : plus la base est grande, plus la corrélation est grande,
jusqu'à la limite d'une base infinie.
. Donc même en gardant le
plus possible l'équivalent des orbitales du dimère nous n'obtenons jamais
de correction BSSE dans la bonne direction, les valeurs dans la base du
dimère sont toujours moins importantes que dans la base des monomères.
Alors la notion du BSSE devient différente : la délocalisation sur l'autre
monomère, avec orbitales localisées ou canoniques, étant plus grand aux
courtes distances, introduit une correction opposée à celle des
autres méthodes de corrélation, pour lesquelles la règle générale
est valable : plus la base est grande, plus la corrélation est grande,
jusqu'à la limite d'une base infinie.
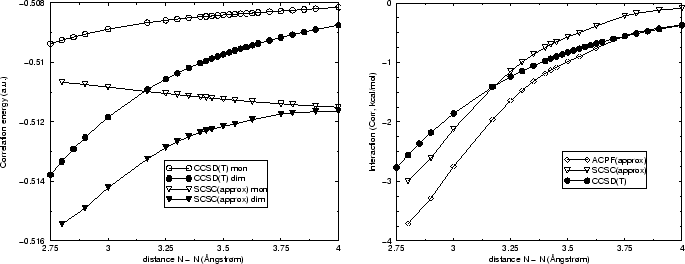
La figure suivante résume de cette discussion, en comparant les courbes
CCSD(T) avec celles de la perturbation Epstein-Nesbet avec habillage (SC)![]() et corrigée ``en F'' par la différence MP2C - MP2L. Les courbes ne
sont pas parallèles, le BSSE inverse contribue à une diminution de
l'écart vers des petites distances. Et clairement l'évolution du BSSE
inverse est visible pour la courbe des monomères. La différence des deux
coubes (dimères et monomères) reste à peu près comparable avec le
calcul CCSD(T), il y a une différence d'environ 0.25
et corrigée ``en F'' par la différence MP2C - MP2L. Les courbes ne
sont pas parallèles, le BSSE inverse contribue à une diminution de
l'écart vers des petites distances. Et clairement l'évolution du BSSE
inverse est visible pour la courbe des monomères. La différence des deux
coubes (dimères et monomères) reste à peu près comparable avec le
calcul CCSD(T), il y a une différence d'environ 0.25![]() kcal/mol. Ceci se
retrouve également avec la version ACPF approchée, même si les valeurs
absolues sont plus importantes dans cette formulation. Dans la limite des
grandes distances ACPF approché montre une très légère erreur de
dissociation; par contre, avec (SC)
kcal/mol. Ceci se
retrouve également avec la version ACPF approchée, même si les valeurs
absolues sont plus importantes dans cette formulation. Dans la limite des
grandes distances ACPF approché montre une très légère erreur de
dissociation; par contre, avec (SC)![]() approché le dimère se dissocie
correctement.
approché le dimère se dissocie
correctement.
 |
Nous obtenons pour le minimum de la courbe du potentiel les valeurs suivantes, à comparer avec la fourchette donnée en Figure 7 :