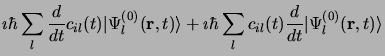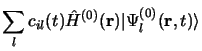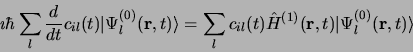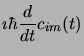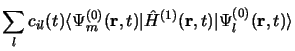suivant: Méthode de variation perturbation.
monter: Perturbation dépendant du temps.
précédent: Perturbation dépendant du temps.
Méthode de variation des constantes.
Considérons un système quantique se trouvant avant la perturbation
(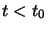 ) dans l'état stationnaire d'énergie
) dans l'état stationnaire d'énergie 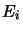 , auquel correspond:
, auquel correspond:
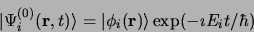 |
(3.73) |
la fonction
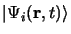 satisfait à l'équation de
Schrödinger dépendant du temps:
satisfait à l'équation de
Schrödinger dépendant du temps:
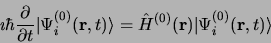 |
(3.74) |
Supposons maintenant, que la perturbation dépendant du temps
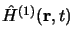 soit appliquée à l'instant
soit appliquée à l'instant 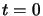 et supprimée à l'instant
et supprimée à l'instant
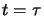 . L'état du système perturbé sera décrit par
. L'état du système perturbé sera décrit par
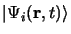 . L'indice
. L'indice 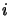 n'est pas relatif à la situation du
système après la perturbation mais, à la situation originelle. La fonction
d'onde
n'est pas relatif à la situation du
système après la perturbation mais, à la situation originelle. La fonction
d'onde
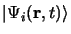 est solution de l'équation de
Schrödinger dépendant du temps:
est solution de l'équation de
Schrödinger dépendant du temps:
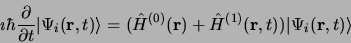 |
(3.75) |
Quand la perturbation est supprimée le système revient à un état
stationnaire et la structure primitive en niveaux d'énergie est rétablie.
Pourtant, si avant la perturbation, le système occupait le 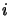 -ième niveau
d'énergie, il peut, une fois celle-ci supprimée occuper le
-ième niveau
d'énergie, il peut, une fois celle-ci supprimée occuper le 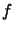 -ième.
Dans ce
cas on dit que la perturbation
-ième.
Dans ce
cas on dit que la perturbation
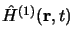 induit la transition
quantique
induit la transition
quantique
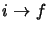 .
.
Le principe de superposition permet de représenter l'état perturbé
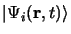 en fonction des états propres de
en fonction des états propres de 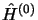 :
:
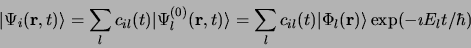 |
(3.76) |
En substituant 3.76 dans 3.75 on obtient:
En éliminant les termes correspondant à l'équation de Schrödinger non
perturbée il reste:
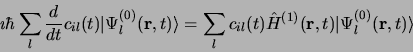 |
(3.78) |
En multipliant à gauche par
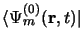 , il vient:
, il vient:
Les coefficients 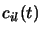 sont alors développés en série
sont alors développés en série
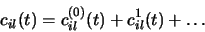 |
(3.80) |
avec
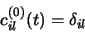 |
(3.81) |
donc
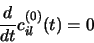 |
(3.82) |
et
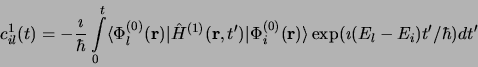 |
(3.83) |



suivant: Méthode de variation perturbation.
monter: Perturbation dépendant du temps.
précédent: Perturbation dépendant du temps.
Bernard Silvi
2005-03-16
![]() -ième niveau
d'énergie, il peut, une fois celle-ci supprimée occuper le
-ième niveau
d'énergie, il peut, une fois celle-ci supprimée occuper le ![]() -ième.
Dans ce
cas on dit que la perturbation
-ième.
Dans ce
cas on dit que la perturbation
![]() induit la transition
quantique
induit la transition
quantique
![]() .
.
![]() en fonction des états propres de
en fonction des états propres de ![]() :
: