


suivant: Théorème d'Hellmann-Feynman
monter: Le théorème du viriel
précédent: Les relations d'Ehrenfest
Théorème du viriel
En appliquant l'équation d'Heisenberg à l'opérateur
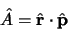 |
(3.29) |
on obtient :
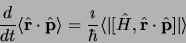 |
(3.30) |
avec
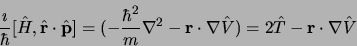 |
(3.31) |
où 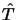 désigne l'opérateur énergie cinétique.
désigne l'opérateur énergie cinétique.
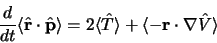 |
(3.32) |
pour un état stationnaire où
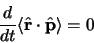 |
(3.33) |
on obtient le théorème du viriel
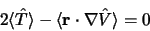 |
(3.34) |
Si l'opérateur énergie potentielle 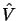 est une fonction homogène de
degré
est une fonction homogène de
degré 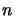 des coordonnées
des coordonnées
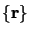 le théorème d'Euler3.1permet d'écrire
le théorème d'Euler3.1permet d'écrire
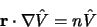 |
(3.35) |
et
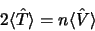 |
(3.36) |
Pour un atome isolé l'opérateur 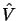 est de degré -1
est de degré -1
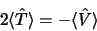 |
(3.37) |



suivant: Théorème d'Hellmann-Feynman
monter: Le théorème du viriel
précédent: Les relations d'Ehrenfest
Bernard Silvi
2005-03-16