


suivant: Théorème du viriel
monter: Le théorème du viriel
précédent: Les relations d'Heisenberg et
La première relation d'Ehrenfest est obtenue en choisissant
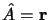 :
:
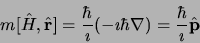 |
(3.24) |
et
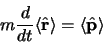 |
(3.25) |
Avec
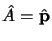
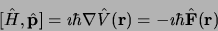 |
(3.26) |
et
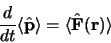 |
(3.27) |
dans cette expression, la deuxième relation d'Ehrenfest,
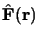 est l'opérateur correspondant à la force.
est l'opérateur correspondant à la force.
En combinant ces deux relations, on obtient une équation analogue à
l'équation de Newton :
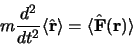 |
(3.28) |
Bernard Silvi
2005-03-16