suivant: La symétrie moléculaire
monter: L'équation de Schrödinger et
précédent: Construction de l'opérateur hamiltonien
La fonction d'onde électronique du système est une fonction des variables 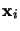 :
:
.
Comme les électrons sont indiscernables, la permutation de deux
quelconques d'entre eux ne modifie pas la situation physique du système. Cette
permutation est réalisée en appliquant l'opérateur de transposition 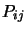 à
la fonction d'onde électronique. L'opérateur de transposition permute avec
l'opérateur hamiltonien parceque d'une part l'addition est commutative et que
d'autre part
à
la fonction d'onde électronique. L'opérateur de transposition permute avec
l'opérateur hamiltonien parceque d'une part l'addition est commutative et que
d'autre part
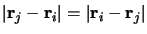 . Les fonctions propres de
. Les fonctions propres de 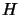 doivent être également fonctions propres
de
doivent être également fonctions propres
de 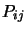 . Désignons par
. Désignons par 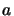 la valeur propre de
la valeur propre de 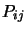 associée à la
fonction propre
associée à la
fonction propre
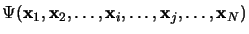 .
.
Les transposition 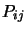 sont des éléments d'un groupe, appelé groupe des
permutations et noté
sont des éléments d'un groupe, appelé groupe des
permutations et noté 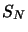 , plus précisément ce sont les générateurs du groupe.
Comme
, plus précisément ce sont les générateurs du groupe.
Comme 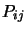 est son propre inverse
est son propre inverse
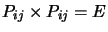 , où
, où 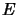 est
l'identité, la valeur de
est
l'identité, la valeur de 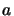 peut être déterminée en appliquant deux fois
peut être déterminée en appliquant deux fois
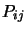 :
:
Ce qui implique:
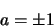 |
(3.14) |
La valeur propre 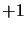 correspond aux système de spin entier, les bosons, tandis
que la valeur propre
correspond aux système de spin entier, les bosons, tandis
que la valeur propre 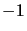 correspond aux fermions (particules de spin
demi-entier). Les éléctrons sont des fermions et la fonction d'onde
électronique est donc antisymétrique par rapport à la permutation des
coordonnées d'espace et de spin de deux électrons quelconques:
correspond aux fermions (particules de spin
demi-entier). Les éléctrons sont des fermions et la fonction d'onde
électronique est donc antisymétrique par rapport à la permutation des
coordonnées d'espace et de spin de deux électrons quelconques:
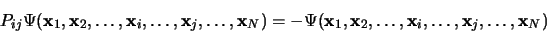 |
(3.15) |
L'équation 3.15 exprime le principe d'antisymétrie ou principe de
Pauli.
Une conséquence importante est que deux électrons de spins paralèlles ne
peuvent pas occuper la même position. Supposons
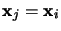 ,
alors
,
alors
relation qui ne peut être vérifiée que si:
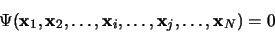 |
(3.17) |
Par contre pour des électrons de spins antiparalèlles
la fonction d'onde ne s'annule pas obligatoirement parceque la divergence
intoduite par l'opérateur 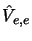 est exactement compensée par
l'énergie cinétique. Physiquement tout se passe comme si les électrons de spins
paralèlles étaient soumis aux coutes distances à un potentiel répulsif plus
fort que le potentiel coulombien classique. Cette contribution purement
quantique est appelée répulsion de Pauli.
est exactement compensée par
l'énergie cinétique. Physiquement tout se passe comme si les électrons de spins
paralèlles étaient soumis aux coutes distances à un potentiel répulsif plus
fort que le potentiel coulombien classique. Cette contribution purement
quantique est appelée répulsion de Pauli.



suivant: La symétrie moléculaire
monter: L'équation de Schrödinger et
précédent: Construction de l'opérateur hamiltonien
Bernard Silvi
2005-03-16