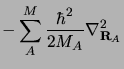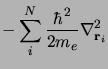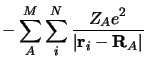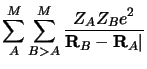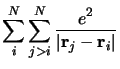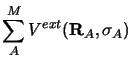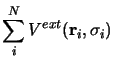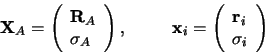suivant: L'indiscernabilité des électrons et
monter: L'équation de Schrödinger et
précédent: L'équation de Schrödinger et
Une molécule est un système quantique constitué de 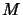 noyaux de masse
noyaux de masse
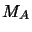 , de charge
, de charge 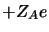 repérés par les vecteurs position
repérés par les vecteurs position 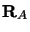 et de
et de 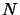 électrons de masse
électrons de masse 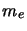 , de charge
, de charge 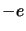 et de position
et de position
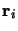 .
Dans le cas le plus général, l'hamiltonien électronique d'un systme
moléculaire s'écrit sous la forme d'une somme de contributions :
.
Dans le cas le plus général, l'hamiltonien électronique d'un systme
moléculaire s'écrit sous la forme d'une somme de contributions :
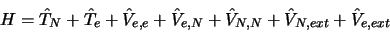 |
(3.1) |
Dans cette expression 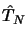 et
et 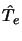 sont les opérateurs énergie
cinétique des noyaux et des électrons qui s'expriment tout deux sous la
forme de sommes de contributions individuelles :
sont les opérateurs énergie
cinétique des noyaux et des électrons qui s'expriment tout deux sous la
forme de sommes de contributions individuelles :
Les opérateurs énergie potentielle électron-noyau, noyau-noyau et
électron-électron sont les sommes des interactions coulombiennes entre
particules chargées :
Enfin 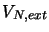 et
et
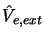 sont les opérateurs de l'énergie
potentielle d'interaction des noyaux et des électrons avec le champ
électromagnétique externe dont nous ne donnons ici que l'expression
formelle :
sont les opérateurs de l'énergie
potentielle d'interaction des noyaux et des électrons avec le champ
électromagnétique externe dont nous ne donnons ici que l'expression
formelle :
afin de faire apparaître les coordonnées de spin 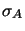 et
et 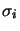 ainsi que le caractère additif de ces potentiels. Même si l'on néglige la
plupart du temps les potentiels de couplage avec un champ externe, leur
expression montre que la fonction d'onde totale solution de l'équation de
Schrödinger est une fonction de
ainsi que le caractère additif de ces potentiels. Même si l'on néglige la
plupart du temps les potentiels de couplage avec un champ externe, leur
expression montre que la fonction d'onde totale solution de l'équation de
Schrödinger est une fonction de 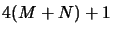 variables :
variables : 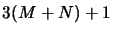 variables
d'espace,
variables
d'espace, 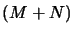 variables de spin et le temps :
variables de spin et le temps :
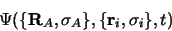 |
(3.9) |
Il est commode de regrouper les coordonnées d'espace et de spin de chaque
particule dans un vecteur à quatre composantes qui sera désigné par
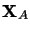 s'il s'agit d'un noyau et par
s'il s'agit d'un noyau et par 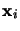 s'il s'agit d'un
électron.
s'il s'agit d'un
électron.
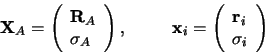 |
(3.10) |
L'équation de Schrödinger dépendant du temps a alors pour expression :
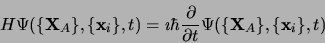 |
(3.11) |
Toutes les fonctions
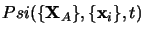 solution de l'équation de Schrödinger dépendant du temps
ne sont pas acceptables du point de vue de la physique. L'interprétation
statistique de la mécanique quantique implique que
solution de l'équation de Schrödinger dépendant du temps
ne sont pas acceptables du point de vue de la physique. L'interprétation
statistique de la mécanique quantique implique que
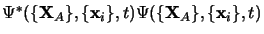 représente la probabilité de trouver le
système au temps
représente la probabilité de trouver le
système au temps 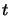 dans la configuration de la donnée des coordonnées
dans la configuration de la donnée des coordonnées
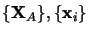 , en d'autre termes
la fonction d'onde doit avoir une valeur finie en tout point de l'espace à
, en d'autre termes
la fonction d'onde doit avoir une valeur finie en tout point de l'espace à
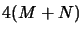 dimensions. L'origine des principales autres conditions sont la nature
des particules, le spin et la symétrie du potentiel nucléaire.
dimensions. L'origine des principales autres conditions sont la nature
des particules, le spin et la symétrie du potentiel nucléaire.



suivant: L'indiscernabilité des électrons et
monter: L'équation de Schrödinger et
précédent: L'équation de Schrödinger et
Bernard Silvi
2005-03-16