


suivant: L'atome d'hydrogène et les
monter: Particule dans un potentiel
précédent: Exercice II.
On considère un système constituée de deux particules de masse
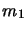 et
et 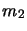 repérées par les vecteurs position
repérées par les vecteurs position 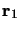 et
et
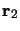 . On appellera
. On appellera 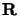 le vecteur position du centre de
gravité et
le vecteur position du centre de
gravité et 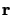 le vecteur
le vecteur
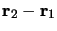 . On supposera
également que ce système est soumis à un potentiel interne
. On supposera
également que ce système est soumis à un potentiel interne
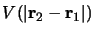
- En faisant l'hypothèse que la fonction d'onde de ce
système peut s'écrire
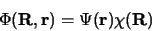 |
(2.88) |
- Écrire les équations différentielles permettant de
déterminer les fonctions
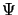 et
et 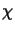 .
.
- Écrire l'équation correspondant à
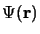 en
coordonnées sphériques en choisissant le centre de gravité
en
coordonnées sphériques en choisissant le centre de gravité 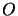 comme origine, les angles
comme origine, les angles 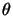 et
et 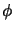 sont les angle polaires
de l'axe du système par rapport à un trièdre arbitraire ayant
sont les angle polaires
de l'axe du système par rapport à un trièdre arbitraire ayant 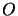 pour origine.
pour origine.
- Montrer que l'opérateur
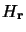 peut s'écrire
peut s'écrire
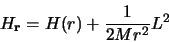 |
(2.89) |
- Donner l'expression des valeurs propres et des fonctions
propres de cet opérateur dans le cas du rotateur rigide (
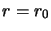 )
)
- On notera les états du rotateur rigide
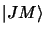 .
L'intensité des transitions dipolaires entre les états
.
L'intensité des transitions dipolaires entre les états
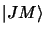 et
et
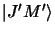 est proportionelle au carré
de l'élément de matrice
est proportionelle au carré
de l'élément de matrice
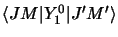
- déduire les valeurs de
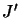 et de
et de 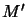 en
fonction de
en
fonction de 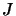 et
et 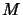 pour lesquelles cette transition est active.
pour lesquelles cette transition est active.



suivant: L'atome d'hydrogène et les
monter: Particule dans un potentiel
précédent: Exercice II.
Bernard Silvi
2005-03-16