


suivant: Matrice inverse.
monter: Matrices.
précédent: Règles pour le produit.
Matrice nulle notée 0 dont tous les éléments sont nuls. Pour
tout 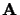 ,
,
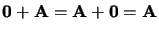 ;
;
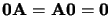 . Toutefois si
. Toutefois si
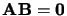 ,
, 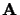 ou
ou 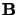 n'est pas nécessairement 0.
n'est pas nécessairement 0.
matrice unité 1,
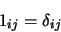 |
(1.5) |
Pour tout 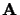
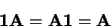 |
(1.6) |
Matrice transposée: 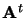
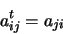 |
(1.7) |
Matrice inverse 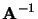
Complexe conjugué d'une matrice 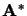 .
.
Matrice associée
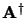 :
:
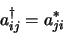 |
(1.8) |
Matrice hermitienne:
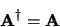 |
(1.9) |
| Relation |
Type de matrice |
propriétés des éléments |
| |
|
|
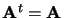 |
symétrique |
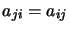 |
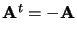 |
antisymétrique |
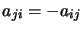
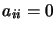 |
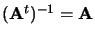 |
orthogonale |
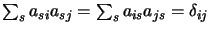 |
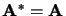 |
réelle |
|
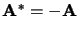 |
imaginaire pure |
|
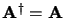 |
hermitienne |
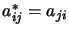 |
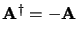 |
antihermitienne |
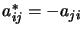 |
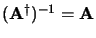 |
unitaire |
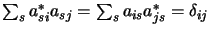 |
| |
|
|



suivant: Matrice inverse.
monter: Matrices.
précédent: Règles pour le produit.
Bernard Silvi
2005-03-16
![]()
![]()
![]() .
.
![]() :
: