


suivant: Opérateurs de projection.
monter: Espace de Hilbert représentation
précédent: Représentation des opérateurs par
La base
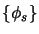 étant complète on peut associer
étant complète on peut associer
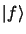 à une fonction
à une fonction 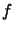 :
:
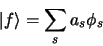 |
(1.92) |
les coefficients 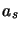 sont les composantes du vecteur
sont les composantes du vecteur
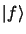 .
.
Si la fonction 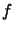 est normée le vecteur
est normée le vecteur
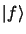 est un vecteur
unitaire:
est un vecteur
unitaire:
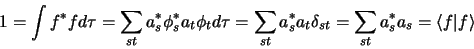 |
(1.93) |
Les intégrales du type
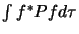 peuvent être
exprimées dans cette notation:
peuvent être
exprimées dans cette notation:
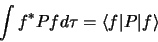 |
(1.94) |
Si 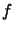 est fonction propre de
est fonction propre de 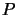 ,
,
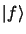 est vecteur propre de
est vecteur propre de 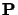
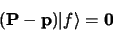 |
(1.95) |
Bernard Silvi
2005-03-16
![]() est normée le vecteur
est normée le vecteur
![]() est un vecteur
unitaire:
est un vecteur
unitaire: