


suivant: Fonctions propres et vecteurs
monter: Espace de Hilbert représentation
précédent: Orthogonalisation canonique.
Si 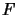 est un opérateur différentiel hermitien ses fonctions
propres
est un opérateur différentiel hermitien ses fonctions
propres 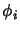 forment un ensemble complet et orthogonal. Introduisons
deux autres opérateurs
forment un ensemble complet et orthogonal. Introduisons
deux autres opérateurs 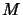 et
et 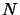 agissant sur le même espace que
agissant sur le même espace que
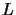 , on définit alors les éléments de matrice:
, on définit alors les éléments de matrice:
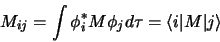 |
(1.84) |
et
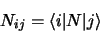 |
(1.85) |
Une propriété intéressante de ces matrices est que les équations
valables pour les opérateurs 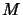 et
et 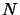 le sont également pour
M et N, en particulier si
le sont également pour
M et N, en particulier si 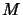 et
et 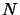 sont linéaires:
sont linéaires:
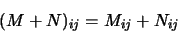 |
(1.86) |
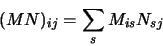 |
(1.87) |
Démonstration: 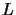 étant un opérateur hermitien ses fonctions
propres forment une base complète, développons
étant un opérateur hermitien ses fonctions
propres forment une base complète, développons
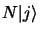 sur cette base que l'on aura normée au préalable
sur cette base que l'on aura normée au préalable
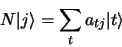 |
(1.88) |
en multipliant à gauche par
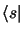 il vient:
il vient:
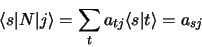 |
(1.89) |
donc
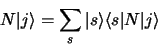 |
(1.90) |
et
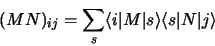 |
(1.91) |
Si l'opérateur 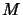 est hermitien la matrice correspondante est
hermitienne.
est hermitien la matrice correspondante est
hermitienne.



suivant: Fonctions propres et vecteurs
monter: Espace de Hilbert représentation
précédent: Orthogonalisation canonique.
Bernard Silvi
2005-03-16
![]() est un opérateur différentiel hermitien ses fonctions
propres
est un opérateur différentiel hermitien ses fonctions
propres ![]() forment un ensemble complet et orthogonal. Introduisons
deux autres opérateurs
forment un ensemble complet et orthogonal. Introduisons
deux autres opérateurs ![]() et
et ![]() agissant sur le même espace que
agissant sur le même espace que
![]() , on définit alors les éléments de matrice:
, on définit alors les éléments de matrice:
![]() est hermitien la matrice correspondante est
hermitienne.
est hermitien la matrice correspondante est
hermitienne.