


suivant: Espace de Hilbert.
monter: Espace de Hilbert représentation
précédent: Espace vectoriel.
Définition: Soit E un espace vectoriel sur le corps
des complexes, ayant pour éléments (vecteurs) 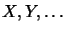 . On dit
que cet espace est normé si à chaque vecteur
. On dit
que cet espace est normé si à chaque vecteur 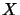 correspond un
nombre réel, noté
correspond un
nombre réel, noté
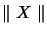 , tel que
, tel que
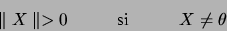 |
(1.60) |
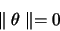 |
(1.61) |
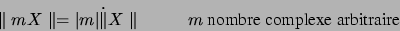 |
(1.62) |
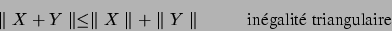 |
(1.63) |
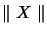 s'appelle norme du vecteur
s'appelle norme du vecteur 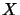 .
.
On dit que l'espace vectoriel E est préhilbertien si l'on
a définit dans E un produit scalaire. A chaque couple
d'éléments 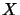 et
et 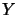 correspond un nombre complexe
correspond un nombre complexe 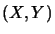 possédant les propriétés suivantes:
possédant les propriétés suivantes:
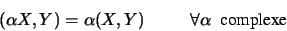 |
(1.64) |
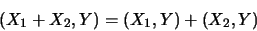 |
(1.65) |
 |
(1.66) |
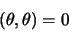 |
(1.67) |
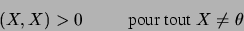 |
(1.68) |
Un espace hilberien est un espace préhilbertien complet, un espace
préhilbertien de dimension finie s'appelle espace hermitien s'il est
complexe et espace euclidien s'il est réel.
Le produit scalaire est utilisé pour définir la norme:
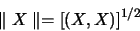 |
(1.69) |



suivant: Espace de Hilbert.
monter: Espace de Hilbert représentation
précédent: Espace vectoriel.
Bernard Silvi
2005-03-16
![]() . On dit
que cet espace est normé si à chaque vecteur
. On dit
que cet espace est normé si à chaque vecteur ![]() correspond un
nombre réel, noté
correspond un
nombre réel, noté
![]() , tel que
, tel que
![]() et
et ![]() correspond un nombre complexe
correspond un nombre complexe ![]() possédant les propriétés suivantes:
possédant les propriétés suivantes: