


suivant: Espace vectoriel norme, espace
monter: Espace de Hilbert représentation
précédent: Espace de Hilbert représentation
On appelle espace vectoriel sur le corps 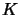 un ensemble E
ayant les propriétés suivantes:
un ensemble E
ayant les propriétés suivantes:
- On peut définir l'addition
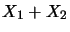 de deux éléments
de E. C'est une opération qui fournit un nouvel élément de
E, et telle que:
de deux éléments
de E. C'est une opération qui fournit un nouvel élément de
E, et telle que:
-
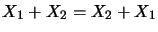 commutativité
commutativité
-
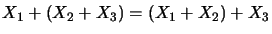 associativité
associativité
- Il existe un élément nul
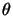 tel que, pour tout
tel que, pour tout
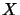 .
.
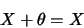 |
(1.50) |
- à tout élément
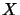 on peut faire correspondre un
élément opposé
on peut faire correspondre un
élément opposé 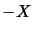
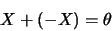 |
(1.51) |
- On peut définir le produit
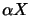 d'un élément
d'un élément 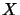 de E par un élément
de E par un élément 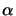 du corps
du corps 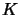 , c'est un
élément de E tel que
, c'est un
élément de E tel que
-
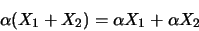 |
(1.52) |
-
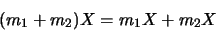 |
(1.53) |
-
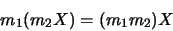 |
(1.54) |
-
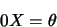 |
(1.55) |
-
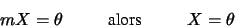 |
(1.56) |
Les élément d'un espace vectoriel sont linéairement dépendants
s'il existe 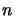 éléments
éléments
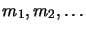 , du corps
, du corps 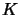 non tous
nuls et tel que:
non tous
nuls et tel que:
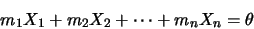 |
(1.57) |
dans le cas contraire les éléments de E sont linéairement
indépendants et
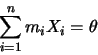 |
(1.58) |
implique que:
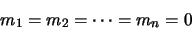 |
(1.59) |
On dit qu'un espace vectoriel est un espace de dimension 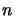 si l'on
peut trouver
si l'on
peut trouver 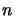 éléments linéairement indépendants mais si
éléments linéairement indépendants mais si
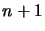 éléments sont toujours linéairement dépendants.
éléments sont toujours linéairement dépendants.
Un ensemble S d'éléments (vecteurs) linéairement
indépendants forment une base de l'espace vectoriel E si tout
élément de E dépend linéairement des vecteurs de
S.



suivant: Espace vectoriel norme, espace
monter: Espace de Hilbert représentation
précédent: Espace de Hilbert représentation
Bernard Silvi
2005-03-16
![]() un ensemble E
ayant les propriétés suivantes:
un ensemble E
ayant les propriétés suivantes:
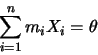
![]() si l'on
peut trouver
si l'on
peut trouver ![]() éléments linéairement indépendants mais si
éléments linéairement indépendants mais si
![]() éléments sont toujours linéairement dépendants.
éléments sont toujours linéairement dépendants.