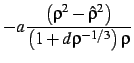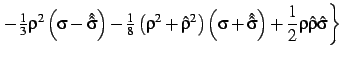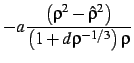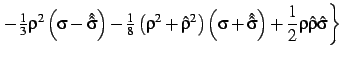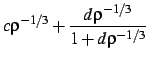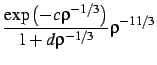Next: 17.1.5 P86: Perdew gradient-corrected
Up: 17.1 Density Functionals
Previous: 17.1.3 VWN: Vosko-Wilk-Nusair (1980)
17.1.4 LYP: Lee-Yang-Parr (1988) gradient-corrected correlation energy
C. Lee, W. Yang and R. G. Parr, Phys. Rev. B 37 (1988) 785;
B. Miehlich, A. Savin, H. Stoll and H. Preuss, Chem. Phys. Letters 157 (1989)
200.
where
and the constants are
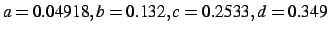 .
.
P.J. Knowles and H.-J. Werner
molpro-support@tc.bham.ac.uk
Mar 8, 2000