Next: 17.1.4 LYP: Lee-Yang-Parr (1988)
Up: 17.1 Density Functionals
Previous: 17.1.2 B: Becke (1988)
17.1.3 VWN: Vosko-Wilk-Nusair (1980) local correlation energy
Can. J. Phys. 58 (1980) 1200.
Define:
Then
where
and each of
 is a function of the
form
is a function of the
form
with the parameters taking the values
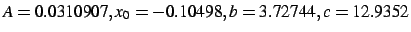 (
(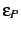 );
);
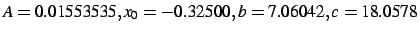 (
(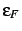 );
);
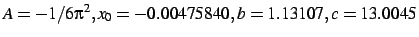 (
(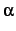 ).
).
Next: 17.1.4 LYP: Lee-Yang-Parr (1988)
Up: 17.1 Density Functionals
Previous: 17.1.2 B: Becke (1988)
P.J. Knowles and H.-J. Werner
molpro-support@tc.bham.ac.uk
Mar 8, 2000
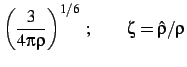
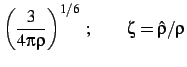
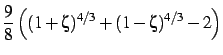
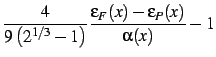
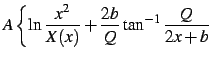
![$\displaystyle \left.
- {bx_0\over X(x_0)}
\left[ \ln{\left(x-x_0\right)^2\over X(x)}
+ {2\left(b+2x_0\right)\over Q}
\tan^{-1} {Q\over 2x+b}\right]\right\}$](img311.gif)