suivant: Exemple :
monter: L'équation de Schrödinger et
précédent: Méthode de variation perturbation
La méthode variationnelle est une autre technique de calcul de fonctions
d'onde approchées dans laquelle le principe variationnel est utilisée pour
minimiser une fonctionnelle dont la valeur est optimale pour la fonction d'onde
exacte.
Les valeurs propres de l'hamiltonien 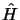 sont classées par ordre
croissant
sont classées par ordre
croissant
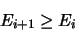 |
(3.103) |
La plus petite valeur propre, 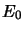 est celle de l'état fondamental. Si
est celle de l'état fondamental. Si
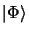 est une fonction d'onde approchée qui peut être
choisie normée, alors
est une fonction d'onde approchée qui peut être
choisie normée, alors
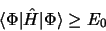 |
(3.104) |
Les fonctions propres
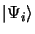 de
de 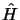 forment une base complète sur laquelle
on développe
forment une base complète sur laquelle
on développe
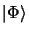 ,
,
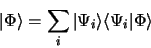 |
(3.105) |
et
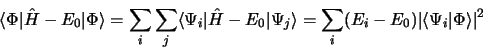 |
(3.106) |
d'où
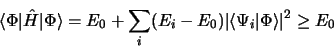 |
(3.107) |
en effet les facteurs apparaissant dans la somme sont tous deux positifs.
L'énergie de l'état fondamental est une borne inférieure à la valeur
moyenne de 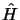 par rapport à une fonction d'onde approchée.
Si
par rapport à une fonction d'onde approchée.
Si
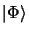 dépend des paramètres
dépend des paramètres
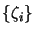 les valeurs optimales de ces paramètres seront celles pour lesquelles
les valeurs optimales de ces paramètres seront celles pour lesquelles
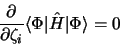 |
(3.108) |
Sous-sections



suivant: Exemple :
monter: L'équation de Schrödinger et
précédent: Méthode de variation perturbation
Bernard Silvi
2005-03-16
![]() sont classées par ordre
croissant
sont classées par ordre
croissant