


suivant: Les fonctions propres des
monter: Représentation matricielle des opérateurs
précédent: Représentation des opérateurs par
Les 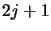 fonctions propres de
fonctions propres de 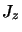 forment une base complète du sous
espace
forment une base complète du sous
espace 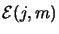 . On peut représenter les kets
. On peut représenter les kets
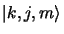 par des vecteurs colonne unitaires dont les composantes sont nulles à
l'exception de celle qui correspond à
par des vecteurs colonne unitaires dont les composantes sont nulles à
l'exception de celle qui correspond à 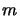 . En ordonnant les kets
. En ordonnant les kets
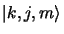 en fonction de
en fonction de 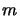 et en désignant l'indice de ligne par
et en désignant l'indice de ligne par 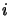 , les
composantes
, les
composantes 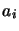 de
de
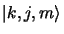 ont pour expression :
ont pour expression :
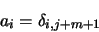 |
(2.54) |
ce qui permet de calculer très facilement les différents éléments de
matrice.
- Élément de matrice de
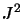 :
:
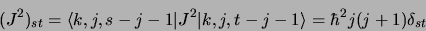 |
(2.55) |
- Élément de matrice de
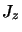 :
:
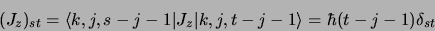 |
(2.56) |
- Élément de matrice de
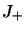 :
:
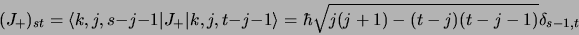 |
(2.57) |
- Élément de matrice de
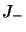 :
:
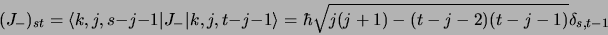 |
(2.58) |
- Élément de matrice de
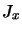 :
:
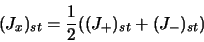 |
(2.59) |
- Élément de matrice de
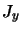 :
:
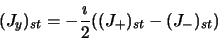 |
(2.60) |



suivant: Les fonctions propres des
monter: Représentation matricielle des opérateurs
précédent: Représentation des opérateurs par
Bernard Silvi
2005-03-16