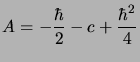suivant: Représentation matricielle des opérateurs
monter: Opérateur moment cinétique et
précédent: Autres relations utiles faisant
Comme nous l'avons démontré précédement si
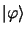 est fonction
propre de
est fonction
propre de 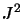 et de
et de 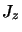 ,
,
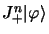 et
et
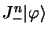 , le sont aussi :
, le sont aussi :
En substituant 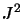 par ses expressions en fonction des produits d'opérateurs
par ses expressions en fonction des produits d'opérateurs
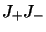 et
et 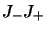 déduites des équations 2.21 et 2.22 :
déduites des équations 2.21 et 2.22 :
on obtient pour 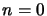
En multipliant à gauche par le bra
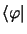 il vient :
il vient :
donc,
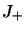 et
et 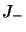 étant complexes conjugués l'un de l'autre, il en est de même
pour
étant complexes conjugués l'un de l'autre, il en est de même
pour
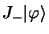 et
et
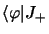 d'une part et
d'une part et
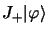 et
et
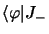 d'autre part et les
produits scalaires
d'autre part et les
produits scalaires
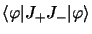 et
et
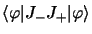 sont positifs ou nuls ce qui
conduits aux inégalités :
sont positifs ou nuls ce qui
conduits aux inégalités :
 |
(2.28) |
Ces inégalités impliquent qu'il existe une valeur maximale, 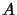 de la valeur
propre
de la valeur
propre
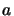 de façon à satisfaire
de façon à satisfaire
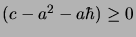 pour
pour 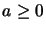 et une valeur
minimale,
et une valeur
minimale, 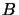 , pour
, pour 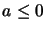 . Ces valeurs propres correspondent aux foctions
propres
. Ces valeurs propres correspondent aux foctions
propres
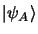 et
et
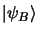 :
:
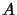 étant la plus grande et
étant la plus grande et 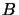 la plus petite valeur propre
la plus petite valeur propre
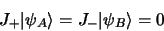 |
(2.30) |
Si les relations ci dessus n'étaient pas satisfaites, alors il
existerait une valeur propre supérieure à 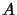 et une valeur propre
inférieure à
et une valeur propre
inférieure à 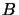 ce qui est contraire aux inégalités de l'équation
2.28. Ces relations impliquent également :
ce qui est contraire aux inégalités de l'équation
2.28. Ces relations impliquent également :
ce qui entraîne 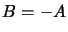 .
le spectre des valeurs propres est donc
.
le spectre des valeurs propres est donc
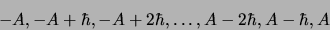 |
(2.32) |
et
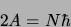 |
(2.33) |
où 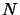 est un entier.
Il existe deux types de valeurs propres selon que
est un entier.
Il existe deux types de valeurs propres selon que 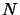 est pair ou impair
est pair ou impair
Dans le premier cas 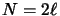 et
et  on a la suite
de valeurs propres :
on a la suite
de valeurs propres :
 |
(2.34) |
Dans le second cas 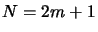 et
et
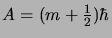 . La séquence
des valeurs propres est :
. La séquence
des valeurs propres est :
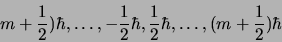 |
(2.35) |
Pour calculer les valeurs propres correspondantes de 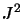 on utilisera
la relation
on utilisera
la relation
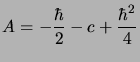 |
|
|
|
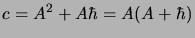 |
|
|
(2.36) |
Dans le cas de la première série de valeurs propres contenant 0 et
dont le moment orbital L est un exemple physique
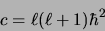 |
(2.37) |
dans l'autre cas auquel correspond par exemple le spin électronique
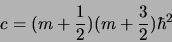 |
(2.38) |



suivant: Représentation matricielle des opérateurs
monter: Opérateur moment cinétique et
précédent: Autres relations utiles faisant
Bernard Silvi
2005-03-16
![]() par ses expressions en fonction des produits d'opérateurs
par ses expressions en fonction des produits d'opérateurs
![]() et
et ![]() déduites des équations 2.21 et 2.22 :
déduites des équations 2.21 et 2.22 :
![]() et
et ![]() on a la suite
de valeurs propres :
on a la suite
de valeurs propres :