


suivant: Commutateurs de et .
monter: Opérateur moment cinétique et
précédent: Hermiticité
On réserve le symbole L au moment cinétique orbital, s au
moment cinétique de spin. On appellera opérateur moment cinétique, noté
J tout opérateur hermitique dont les composantes satisfont les
relations de commutation :
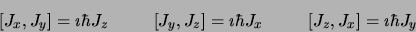 |
(2.12) |
de plus :
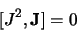 |
(2.13) |
On définit les opérateurs 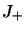 et
et 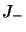 par les relation suivantes :
par les relation suivantes :
 |
(2.14) |
Ces opérateurs jouent un rôle semblable à celui des opérateurs 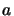 et
et
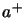 introduits pour étudier l'oscillateur harmonique. Remarquons tout d'abord
que
introduits pour étudier l'oscillateur harmonique. Remarquons tout d'abord
que 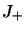 et
et 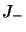 commuttent avec
commuttent avec 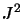 :
:
ce qui implique que si
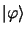 est une fonction propre de
est une fonction propre de 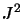 :
:
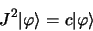 |
(2.16) |
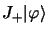 et
et
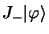 sont également
fonctions propres de
sont également
fonctions propres de 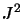 avec la même valeur propre
avec la même valeur propre 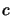
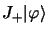 et
et
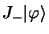 sont également
fonctions propres de
sont également
fonctions propres de 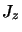 :
:
En répétant 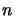 fois l'action de
fois l'action de 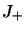 ou de
ou de 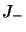 sur
sur
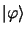 on obtient les relations générales :
on obtient les relations générales :
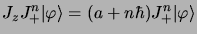 |
|
|
|
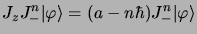 |
|
|
(2.19) |
Sous-sections



suivant: Commutateurs de et .
monter: Opérateur moment cinétique et
précédent: Hermiticité
Bernard Silvi
2005-03-16