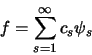suivant: Définition : Une base
monter: Propriétés des fonctions propres
précédent: Propriétés des fonctions propres
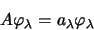 |
(1.39) |
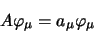 |
(1.40) |
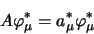 |
(1.41) |
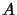 étant hermitien
étant hermitien 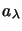 et
et 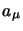 sont réelles
sont réelles
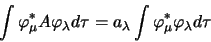 |
(1.42) |
d'autre part
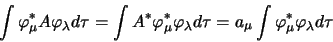 |
(1.43) |
donc
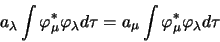 |
(1.44) |
Cette égalité ne peut être vérifiée que si
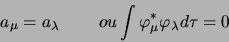 |
(1.45) |
On appelle ensemble complet un ensemble de fonctions de mêmes variables
et de carré sommable
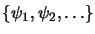 tel que
pour toute fonction
tel que
pour toute fonction 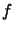 de mêmes variables et de carré sommable
de mêmes variables et de carré sommable
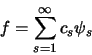 |
(1.46) |
Théorème : Les fonctions propres d'un opérateur hermitien
forment un ensemble complet. Cet ensemble est également appelé
base.



suivant: Définition : Une base
monter: Propriétés des fonctions propres
précédent: Propriétés des fonctions propres
Bernard Silvi
2005-03-16