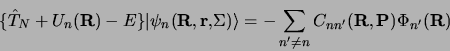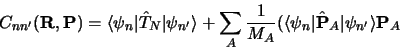suivant: Approximation adiabatique
monter: L'équation de Schrödinger et
précédent: Matrices densité.
Une molécule est constituée de deux types de particules :
- les noyaux de masse
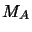 , de charge
, de charge 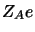 , qui peuvent être
des
fermions ou des bosons
, qui peuvent être
des
fermions ou des bosons
- les électrons de masse
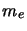 , de charge
, de charge 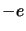 qui sont des
fermions.
qui sont des
fermions.
En unités atomiques, l'hamiltonien correspondant à un tel système
a pour
expression :
L'opérateur 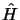 classique dépend uniquement des variables
d'espace :
les coordonnées
classique dépend uniquement des variables
d'espace :
les coordonnées
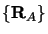 des noyaux et
des noyaux et
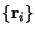 des
électrons. Le caractère fermionique ou bosonique des particules
n'apparait
pas dans l'opérateur.
des
électrons. Le caractère fermionique ou bosonique des particules
n'apparait
pas dans l'opérateur.
Le premier problème à résoudre va être d'essayer de séparer
le
mouvement des noyaux de celui des électrons. Ceci est d'autant plus
justifié que ces particules ont des masses très différentes et
qu'elles
peuvent avoir des spins différents. 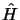 peut être décomposé
en
une contribution cinétique purement nucléaire
peut être décomposé
en
une contribution cinétique purement nucléaire 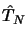 et un
hamiltonien
électronique :
et un
hamiltonien
électronique :
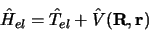 |
(3.117) |
qui est un opérateur hermitique paramétrique en 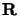 .
L'ensemble de
ses fonctions propres
.
L'ensemble de
ses fonctions propres
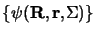 -
- 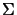 désigne l'ensemble des variables de spin électronique
désigne l'ensemble des variables de spin électronique 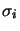 -
forme une base complète sur laquelle on pourra développer la
fonction
d'onde totale du système
-
forme une base complète sur laquelle on pourra développer la
fonction
d'onde totale du système
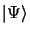
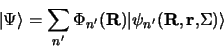 |
(3.118) |
où les 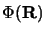 sont des coefficients paramètriques. En
substituant
dans l'équation de Schrödinger totale on obtient :
sont des coefficients paramètriques. En
substituant
dans l'équation de Schrödinger totale on obtient :
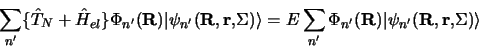 |
(3.119) |
comme :
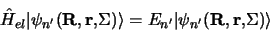 |
(3.120) |
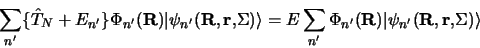 |
(3.121) |
en multipliant à gauche par
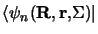 on obtient :
on obtient :
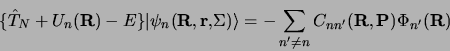 |
(3.122) |
avec :
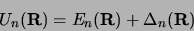 |
(3.123) |
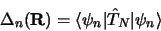 |
(3.124) |
et
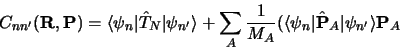 |
(3.125) |
A cause du second membre on doit connaître le spectre complet des
états
propres de 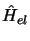 .
.
Sous-sections



suivant: Approximation adiabatique
monter: L'équation de Schrödinger et
précédent: Matrices densité.
Bernard Silvi
2005-03-16
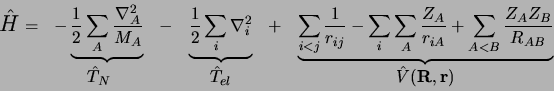
![]() classique dépend uniquement des variables
d'espace :
les coordonnées
classique dépend uniquement des variables
d'espace :
les coordonnées
![]() des noyaux et
des noyaux et
![]() des
électrons. Le caractère fermionique ou bosonique des particules
n'apparait
pas dans l'opérateur.
des
électrons. Le caractère fermionique ou bosonique des particules
n'apparait
pas dans l'opérateur.
![]() peut être décomposé
en
une contribution cinétique purement nucléaire
peut être décomposé
en
une contribution cinétique purement nucléaire ![]() et un
hamiltonien
électronique :
et un
hamiltonien
électronique :