where
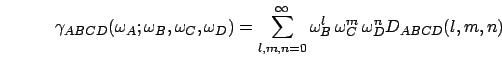 which for
which for  are defined by the expansion
are defined by the expansion

In the *CCCR section the input that is specific for coupled cluster cubic response properties is read in. This section includes:
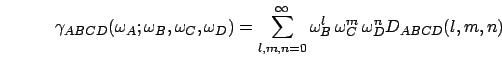 which for
which for  are defined by the expansion
are defined by the expansion

The response functions are evaluated for a number of operator quadruples (specified with the keywords .OPERAT, .DIPOLE, or .AVERAG) which are combined with triples of frequency arguments specified using the keywords .MIXFRE, .THGFRE, .ESHGFR, .DFWMFR, .DCKERR, or .STATIC. The different frequency keywords are compatible and might be arbitrarely combined or repeated. For dispersion coefficients use the keyword .DISPCF.
READ (LUCMD,'(A)') AVERAGE
READ (LUCMD,'(A)') SYMMETRY
Evaluate special tensor averages of cubic response functions.
Presently implemented are the isotropic averages of the second
dipole hyperpolarizability
![]() and
and ![]() .
Set
.
Set AVERAGE to GAMMA_PAR
to obtain ![]() and to
and to
GAMMA_ISO to obtain ![]() and
and ![]() .
The
.
The SYMMETRY input defines the selection rules
exploited to reduce the number of tensor elements that have to be
evaluated. Available options are
ATOM, SPHTOP (spherical top), LINEAR,
and GENER (use point group symmetry from geometry input).
Note that the .AVERAG option should be specified in the *CCCR
section before any .OPERAT or .DIPOLE input.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (DCRFR(IDX),IDX=NCRFREQ+1,NCRFREQ+MFREQ)
Input for dc-Kerr effect
![]() :
on the first line following .DCKERR the number of different
frequencies are read, from the second line the input for
:
on the first line following .DCKERR the number of different
frequencies are read, from the second line the input for
![]() is read.
is read. ![]() and
and ![]() to
to ![]() and
and ![]() to
to ![]() .
.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (BCRFR(IDX),IDX=NCRFREQ+1,NCRFREQ+MFREQ)
Input for degenerate four wave mixing
![]() :
on the first line following .DFWMFR the number of different
frequencies are read, from the second line the input for
:
on the first line following .DFWMFR the number of different
frequencies are read, from the second line the input for
![]() is read.
is read. ![]() is set to
is set to ![]() ,
,
![]() and
and ![]() to
to ![]() .
.
READ (LUCMD,*) NCRDSPE
Calculate the dispersion coefficients
![]() up to
up to
![]()
NCRDSPE.
Note that dispersion coefficients presently are only available for
real fourth-order properties.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (BCRFR(IDX),IDX=NCRFREQ+1,NCRFREQ+MFREQ)
Input for electric field induced second harmonic generation
![]() :
on the first line following .ESHGFR the number of different
frequencies are read, from the second line the input for
:
on the first line following .ESHGFR the number of different
frequencies are read, from the second line the input for
![]() is read.
is read. ![]() is set to
is set to ![]() ,
,
![]() to
to ![]() and
and ![]() to
to ![]() .
.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (BCRFR(IDX),IDX=NCRFREQ+1,NCRFREQ+MFREQ)
READ (LUCMD,*) (CCRFR(IDX),IDX=NCRFREQ+1,NCRFREQ+MFREQ)
READ (LUCMD,*) (DCRFR(IDX),IDX=NCRFREQ+1,NCRFREQ+MFREQ)
Input for general frequency mixing
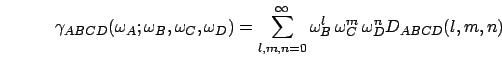 : on the first line
following .MIXFRE the number of differenct frequencies
is read and from the next three lines the frequency arguments
: on the first line
following .MIXFRE the number of differenct frequencies
is read and from the next three lines the frequency arguments
![]() ,
, ![]() , and
, and ![]() are read
(
are read
(![]() is set to
is set to
![]() ).
).
READ (LUCMD,'(4A)') LABELA, LABELB, LABELC, LABELD
DO WHILE (LABELA(1:1).NE.'.' .AND. LABELA(1:1).NE.'*')
READ (LUCMD,'(4A)') LABELA, LABELB, LABELC, LABELD
END DO
Read quadruples of operator labels. For each of these operator quadruples the cubic response function will be evaluated at all frequency triples. Operator quadruples which do not correspond to symmetry allowed combination will be ignored during the calculation.
READ (LUCMD,*) IPRINT
Set print parameter for the cubic reponse section.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (BCRFR(IDX),IDX=NCRFREQ+1,NCRFREQ+MFREQ)
Input for third harmonic generation
![]() :
on the first line following .THGFRE the number of different
frequencies is read, from the second line the input for
:
on the first line following .THGFRE the number of different
frequencies is read, from the second line the input for
![]() is read.
is read. ![]() and
and ![]() are set to
are set to
![]() and
and ![]() to
to ![]() .
.
 -vectors as intermediates
-vectors as intermediates