where
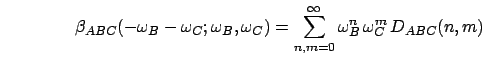 for third-order properties,
which for
for third-order properties,
which for  are defined by the expansion
are defined by the expansion

In the *CCQR section you specify the input for coupled cluster quadratic response calculations. This section includes:
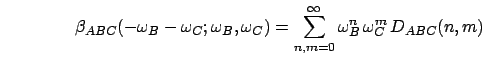 for third-order properties,
which for
for third-order properties,
which for  are defined by the expansion
are defined by the expansion

The response functions are evaluated for a number of operator triples (given using the .OPERAT, .DIPOLE, or .AVERAG keywords) which are combined with pairs of frequency arguments specified using the keywords .MIXFRE, .SHGFRE, .ORFREQ, .EOPEFR or .STATIC. The different frequency keywords are compatible and might be arbitrarily combined or repeated. For dispersion coefficients use the keyword .DISPCF.
READ (LUCMD,'(A)') LINE
Evaluate special tensor averages of quadratic response properties.
Presently implemented are only the vector averages of the first
dipole hyperpolarizability ![]() ,
, ![]() and
and
![]() . All three of these averages are obtained if
. All three of these averages are obtained if
HYPERPOL is specified on the input line that follows
.AVERAG.
The .AVERAG keyword should be used before any .OPERAT
or .DIPOLE input in the *CCQR section.
READ (LUCMD,*) NQRDSPE
Calculate the dispersion coefficients
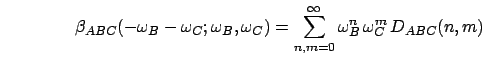 up to order
up to order ![]()
NQRDSPE.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (BQRFR(IDX),IDX=NQRFREQ+1,NQRFREQ+MFREQ)
Input for the electro optical Pockels effect
![]() :
on the first line following .EOPEFR the number of different
frequencies is read, from the second line the input for
:
on the first line following .EOPEFR the number of different
frequencies is read, from the second line the input for
![]() is read.
is read. ![]() is set to
is set to ![]() and
and
![]() to
to
![]() .
.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (BQRFR(IDX),IDX=NQRFREQ+1,NQRFREQ+MFREQ)
READ (LUCMD,*) (CQRFR(IDX),IDX=NQRFREQ+1,NQRFREQ+MFREQ)
Input for general frequency mixing
![]() : on the first line
following .MIXFRE the number of different frequencies
(for this keyword) is read, from the second and third line
the frequency arguments
: on the first line
following .MIXFRE the number of different frequencies
(for this keyword) is read, from the second and third line
the frequency arguments ![]() and
and ![]() are read
(
are read
(![]() is set to
is set to
![]() ).
).
READ (LUCMD'(3A)') LABELA, LABELB, LABELC
DO WHILE (LABELA(1:1).NE.'.' .AND. LABELA(1:1).NE.'*')
READ (LUCMD'(3A)') LABELA, LABELB, LABELC
END DO
Read triples of operator labels. For each of these operator triples the quadratic response function will be evaluated at all frequency pairs. Operator triples which do not correspond to symmetry allowed combination will be ignored during the calculation.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (BQRFR(IDX),IDX=NQRFREQ+1,NQRFREQ+MFREQ)
Input for optical rectification
![]() :
on the first line following .ORFREQ the number of different
frequencies is read, from the second line the input for
:
on the first line following .ORFREQ the number of different
frequencies is read, from the second line the input for
![]() is read.
is read. ![]() is set to
is set to
![]() and
and
![]() to
to ![]() .
.
READ (LUCMD,*) IPRINT
Set print parameter for the quadratic response section.
READ (LUCMD,*) MFREQ
READ (LUCMD,*) (BQRFR(IDX),IDX=NQRFREQ+1,NQRFREQ+MFREQ)
Input for second harmonic generation
![]() :
on the first line following .SHGFRE the number of different
frequencies is read, from the second line the input for
:
on the first line following .SHGFRE the number of different
frequencies is read, from the second line the input for
![]() is read.
is read. ![]() is set to
is set to ![]() and
and ![]() to
to ![]() .
.