Théorie Heitler-London et DFT

Considérons maintenant une méthode alternative pour remplacer des termes lourds à calculer en SAPT : la décomposition Heitler-London et la DFT. Dans cette approche la décomposition est effectu'ee en trois étapes :

• première étape : le calcul de l'interaction électrostatique à partir des fonctions d'onde originales des monomères, c'est-à-dire ni relaxées, ni antisymétrisées.
• deuxième étape : l'antisymétrisation complète du produit des fonctions d'ondes des monomères permet de calculer la répulsion d'échange ou de Pauli. La répulsion resulte de l'augmentation de l'énergie cinétique lors de la modification de la densité électronique par antisymétrisation. Les électrons de même spin évitent de peupler la zone entre les monomères et se concentrent autour des noyaux et dans les régions hors de la zone de recouvrement. Après les deux étapes nous avons une interaction analogue à l'approximation de W. Heitler et F. London.[#!HeitlerLondon!#]
• troisième étape : relaxation des orbitales vers la solution Hartree-Fock du dimère : interaction orbitalaire. La zone entre les monomères redevient peuplée; cette relaxation s'accompagne d'une baisse de l'énergie cinétique.

En utilisant des orbitales Kohn-Sham de la DFT au lieu d'orbitales Hartree-Fock, on obtient une décomposition analogue, mais tenant compte de la corrélation électronique intra-moléculaire et inter-moléculaire. Les étapes du calcul suivent le schéma proposé par M. Bickelhaupt et E. J. Baerends,[#!Bickelhaupt!#] et utilisé par ces auteurs pour décrire les liaisons chimiques et la liaison hydrogène.[#!Fonseca!#] Cette décomposition est implémentée dans le code ADF (Amsterdam Density Functional),[#!ADF!#] pour les fonctionnelles LDA,[#!LDA!#] BLYP[#!BLYP!#] et PW91.[#!PW91!#] Dans ce logiciel les orbitales moléculaires sont développées sur des bases numériques ou des bases de fonctions Slater.

Pour exploiter d'autres fonctionnelles, et pour pouvoir comparer les résultats avec les calculs SAPT, où la base de développement des orbitales moléculaires sont des fonctions gaussiennes, j'ai intégré le schéma dans le module SCF de mes programmes, en faisant appel aux routines DFT du package MOLPRO.[#!MOLPRO!#]

La comparaison avec les termes SAPT est directe pour la première étape, qui fait interagir les densités électroniques des monomères sans corrélation intramoléculaire (niveau Hartree-Fock) ou avec corrélation intramoléculaire (niveau DFT). La décomposition en échange, dispersion et induction est plus difficile parce que la dispersion n'a pas de place explicite dans la DFT. Nous pourrons comparer la ``répulsion de Pauli'' avec l'échange au premier ordre en SAPT (E$_{exch}^{(1)}$) et l'interaction orbitalaire avec la somme de dispersion et induction. Comme il n'y a pas de fondement théorique rigoureux et commun entre les deux approches SAPT et DFT, nous pouvons essayer des expériences numériques en regroupant des termes différament.

Nous avons observé ainsi un chose surprenante : parmis la multitude de fonctionnelles sur le marché, la fonctionnelle Perdew-Wang 91[#!PW91!#] semble reproduire la dispersion de SAPT dans le terme ``répulsion de Pauli''.

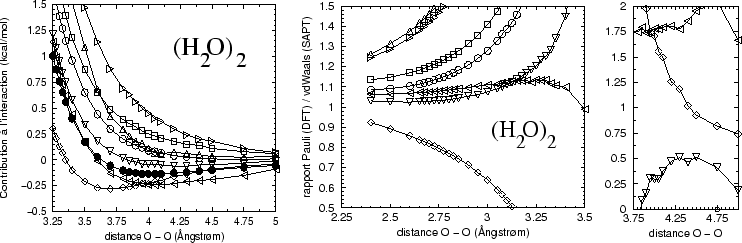
Il faut d'abord remarquer que ce terme n'est pas toujours positif pour cette fonctionnelle (Fig. 17), mais montre un petit creux comme un minimum van der Waals.

Alors nous pouvons comparer la ``répulsion de Pauli'' avec une somme de termes en SAPT correspondant à des interactions van der Waals seulement, sans interaction électrostatique ni induction

$$E_{vdWaals}=\left[E_{exch-rep}^{(10)}+ E _{exch}^{(1)}({\te... ...^{(21)}+E_{disp}^{(22)} + E_{exch-disp}^{(20)}\right] \qquad .$$ (27)

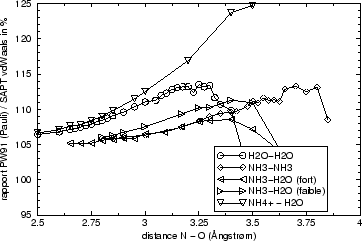
Le rapport entre le terme ``répulsion de Pauli'' de la décomposition DFT et la contribution ``van der Waals'' en SAPT est rélativement proche de 1 pour la fonctionnelle PW91, contrairement aux autres fonctionnelles, du moins lorsque la distance intermoléculaire n'est pas trop longue. Ce rapport n'est plus une bonne quantité lors du passage par zéro de $E_{vdWaals}$ de SAPT, et au delà la précision du calcul d'un coté, et l'incapacité de la DFT de décrire des éffets de dispersion à longue portée de l'autre coté font que la comparaison a des limites. true cm

Figure 17: Comparaison de $E_{vdWaals}$ (SAPT) avec la ``répulsion de Pauli'' (DFT) avec différentes fonctionnelles pour le dimère de l'eau. La contribution à l'interaction est donnée à gauche; au milieu figure le rapport DFT/SAPT pour des distances où la contribution est répulsive, et à droite le même rapport dans la partie attractive. Les différentes fonctionnelles sont BLYP[#!BLYP!#] ($\Box -\Box$), LDA[#!LDA!#] ( $\Diamond -\Diamond$), VSXC[#!VSXC!#] ( $\triangle -\triangle$), PW91[#!PW91!#] ($\lhd -\lhd$), PBE0[#!PBE!#] ( $\bigtriangledown -\bigtriangledown$), BW[#!BW!#] ($\rhd -\rhd$) et Hartree-Fock ($\circ -\circ$). Les symboles pleins ( $\bullet - \bullet$) à gauche représentent la référence SAPT.

true cm

Figure 18: Rapport ``répulsion de Pauli''(DFT)/$E_{vdWaals}$ (SAPT) avec la fonctionnelle PW91 et pour cinq dimères H$_2$O$\cdots$H$_2$O, NH$_3\cdots$NH$_3$, HNH$_2\cdots$H$_2$O, HOH$\cdots$NH$_3$ et NH$_4^+\cdots$H$_2$O.

La prise en compte des termes d'échange des corrections de corrélation intramoléculaire à la dispersion ( $E_{disp}^{(21)}$ et $E_{disp}^{(22)}$), indisponible dans le programme actuel, pourrait corriger la contribution van der Waals et améliorer le rapport ``répulsion de Pauli (DFT) / van der Waals (SAPT)''.

Nous avons observé le même effet pour cinq dimères différents et nous doutons que le résultat soit dû à une pure coincidence, même si nous sommes pour l'instant incapables de donner une raison plus fondée.

En fait nous sommes conscients que la méthode SAPT telle qu'elle existe actuellement ne contient pas tous les termes de corrélation intramoléculaires. Il nous a donc paru intéressant d'avoir une idée de la valeur des termes manquants dans cette méthode. Nous pouvons même imaginer une méthode ``hybride'' qui contiendrait des termes SAPT et des termes qui seraient calculés comme différences DFT/SAPT, voir le tableau VII.

$$% latex2html id marker 3198\begin{minipage}{13 true cm} \b... ....) -- HF(Int.Orb.)) \\ \end{tabular}\end{table}\end{minipage}$$

Afin de vérifier nos hypothèse nous avons appliqué les expressions du tableau VII au dimère de NH$_3$ du chapitre précédent, pour lequel certains termes SAPT ont été recalculé. Parmi les nombreuses fonctionnelles disponibles nous avons retenu dans cette étude BLYP, PW91 et PBE0. Cette dernière est construite à l'aide de conditions analytiques pour faibles et fortes densités et elle inclue un terme d'échange exact.[#!PBE!#] En absence de critères de sélection plus fondés, nous pourrons expérimenter et voir, si la reconstruction des contributions de SAPT est faisable en combinant les résultats des différentes fonctionnelles.

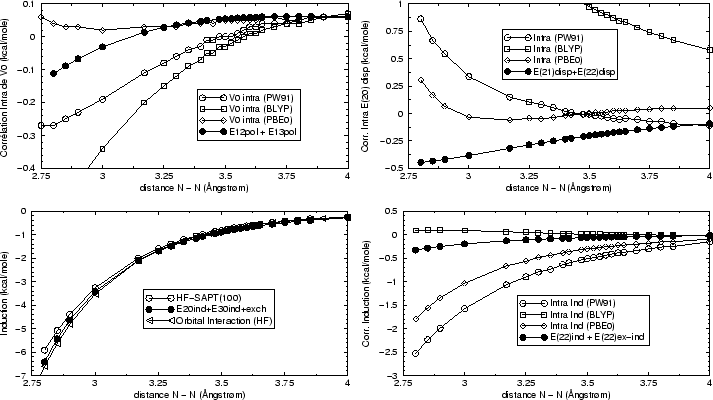
Les approximations apportées sont (Figure 19) visiblement trop importantes pour justifier une modélisation directe des contributions SAPT coûteuses. D'autre part, la figure montre qu'une fois de plus le choix de la fonctionnelle a une grande influence sur les formes des contributions. Une analyse plus fine permettra peut-être un jour d'estimer l'ordre de grandeur et le signe des contributions SAPT manquantes (d'échange ou d'ordres supérieurs), ou bien, de façon complémentaire de construire de nouvelles fonctionnelles en profitant des données présentées ici. Toutefois nous pouvons constater que l'ordre de grandeur de l'erreur sur les différents termes est d'environ 0.25$$kcal/mole pour les deux premières reconstructions de la figure 19, et plus grand pour la corrélation intramolculaire sur le terme d'induction.

Figure 19: La reconstruction des termes comme différences entre expressions DFT et SAPT ou Hartree-Fock. Les fonctionnelles utilisées sont PW91, B-LYP et PBE0. En haut à gauche se trouve la corrélation intra-moléculaire de l'interaction électrostatique, en haut à droite la corrélation intra-moléculaire de la dispersion, en bas à gauche l'induction Hartree-Fock, et en bas à droite la corrélation intra-moléculaire de l'induction.

Finalement nous pourrons construire ainsi l'interaction complète à partir des reconstructions de la figure précédente, en utilisant les résultats les plus proches de la référence SAPT. Cela revient à choisir la corrélation intramoléculaire de V$_0$ par V$_0$(intra) PW91, la corrélation intramoléculaire de la dispersion PBE0 l'interaction orbitalaire de Hartree-Fock, et finalement l'interaction orbitalaire BLYP pour introduire la corrélation intramoléculaire de l'induction. A cela s'ajoutent les contributions à calculer par Hartree-Fock et SAPT du tableau VII.

Cette recette élaborée à l'aide de (NH$_3$)$_2$ devrait être confirmée par des calculs sur d'autres systèmes. Mais la variation des résultats en fonction du choix de la fonctionnelle est tellement grande, qu'il faudrait peut-être attendre l'élaboration d'autres fonctionnelles specifiquement conçues pour des interactions intermoléculaires comme le PBE0AC[#!PBE0AC!#] avec corrections asymptotiques.

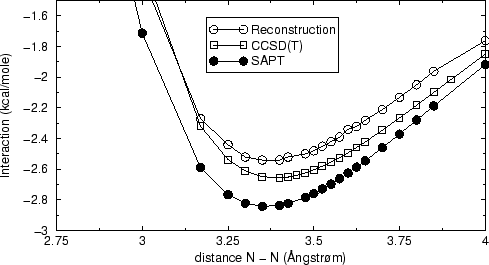
La figure 20 montre que le mélange de fonctionnelles et SAPT peut conduire à une courbe de potentiel raisonnable, malgré les différences entre SAPT et ses reconstructions pour les contributions individuelles de figure 19. Les différences d'énergie, par rapport à CCSD(T) supermoléculaire et SAPT sont de l'ordre de 0.5$$kcal/mole et la position du minimum est au même endroit avec les trois méthodes.

Figure 20: Courbes de potentiel intermoléculaire SAPT, CCSD(T) et reconstruction de SAPT à l'aide de la DFT. Les minima correspondent à $R_e=3.362$Å et $E_{int}=-2.843$kcal/mol (SAPT), $R_e=3.389$Å et $E_{int}=-2.656$kcal/mol (CCSD(T)) et à $R_e=3.380$Å et $E_{int}=-2.543$kcal/mol (SAPT approché).

Cette voie de recherche empirique peut néanmoins apporter du sens physique aux démarches théoriques rigoureuses, présentées dans le chapitre précédent. L'approche CCSD(T) que nous avons utilisée comme référence du potentiel intermoléculaire ne fournit que ce potentiel total, sans aucune information supplémentaire.

La DFT étant une méthode parametrée en cherchant de respecter des valeurs limites et de reproduire le plus possible la densité et l'énergie de l'état fondamental d'un système ne donne pas non plus à priori des détails des potentiels intermoléculaires.

Ce n'est qu'en interaction avec d'autres méthodes tels que SAPT ou les méthodes Monte Carlo et modèles physiques (n'oublions pas l'expérience) que les fonctionnelles utilisées quotidiennement peuvent être améliorées et que leur capacités peuvent être discutées.

=1