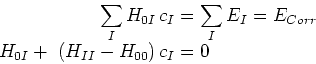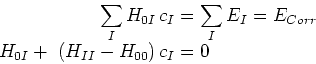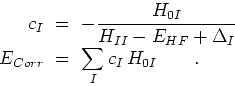Approximation diagonale

Si on met les eléments hors la diagonale à zéro, on obtient de CEPA-0 la perturbation Epstein-Nesbet (exercice dans le livre de Szabo and Ostlund)

$$\begin{eqnarray*} \sum_I H_{0I} c_I & = & \sum_I E_I = E_{Corr} \cr H_{0I} + (H_{II}-H_{00}) c_I & = & 0 \end{eqnarray*}$$

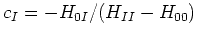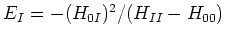amène directement à $c_I=-H_{0I}/(H_{II}-H_{00})$ et $E_I =-(H_{0I})^2/(H_{II}-H_{00})$, i.e. l'énergie Epstein-Nesbet en 2e ordre.

Bien sûr, tous les habillages présentés auparavant peuvent être utilisés, pour calculer l'énergie de corrélation par

$$\begin{eqnarray*} c_I & = & -{{H_{0I}}\over{H_{II}-E_{HF}+\Delta_I}} \cr E_{Corr} & = & \sum_I c_I H_{0I} \qquad . \end{eqnarray*}$$

La procédure est itérative puisque l'habillage 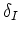$\delta_I$ dépend des coefficients 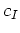$c_I$. En général, l'autocohérence est obtenu au bout de quelques cycles.

En orbitales localisées cette corrélation Epstein-Nesbet n'est pas tout : il manque l'ensemble de diagrammes impliquant les éléments non-diagonaux de l'opérateur de Fock. Un façon simple d'ajouter l'essentiel est de considérer la différence entre MP2 en orbitales localisées et MP2 en orbitales canoniques (option MP2CAN). Une énergie comparable à l'IC habillée est obtenu par

$$E_{Corr} \approx E({\text{EN2, habill\'e}})+E({\text{MP2CAN}}) - E({\text{MP2}}) \qquad .$$