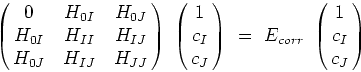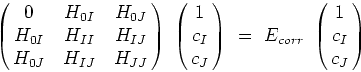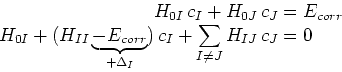Next: Approximation diagonale
Up: Le programme d'ICSD en
Previous: Le programme d'ICSD en
L'idée de base dans ce chapitre est le fait que tout problème à valeur
propre peut être écrit comme un système d'équations linéaires, et
vice versa. Kutzelnigg démontrait cela pour le LCCSD dans
W.Kutzelnigg, Chem.Phys.Lett., 35 (1975) 283, et l'équivalence
``full CEPA'' and ``self-consistent size-consistent CI'' a été
développée dans J.-P.Daudey, J.-.L.Heully, J.-P.Malrieu, J.Chem.Phys., 99 (1993) 1240.
Le problème à valeur propre de l'IC
devient
ce qui est un système d'équations linéaires avec un habillage diagonal
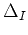 pour chaque déterminant
pour chaque déterminant 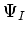 . Nous partons du CEPA-0 qui
est la sommation infinie de toutes les doubles excitations dans la série de
perturbations, avec
. Nous partons du CEPA-0 qui
est la sommation infinie de toutes les doubles excitations dans la série de
perturbations, avec 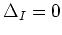 pour tous les déterminants..
pour tous les déterminants..
Moyenner les effets de l'habillage sur tous les déterminants donne l'ACPF
(Gdanitz, Ahlrichs) et l'AQCC de Szalay and Bartlett.
Peter Reinhardt
2008-05-14