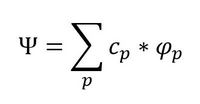Quelques précisions et précautions
Rappelons que les calculs sont effectués en général au niveau AM1.
C’est une méthode autocohérente semi-empirique, simple mais robuste, qui ne
traite explicitement que les électrons de valence (on trouvera quelques
précisions à l’adresse HartreeFock.pdf, page 7). En raison des simplifications et approximations qu’elle comporte, les résultats ont un caractère essentiellement comparatif et donc non absolu notamment :
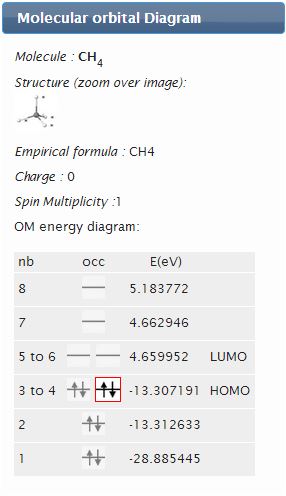
- L’énergie des orbitales occupées correspond approximativement à l’opposé de l’énergie d'ionisation. Bien que
sans interprétation théorique, l'énergie
de l'orbitale vacante de plus basse énergie est empiriquement corrélée à l’affinité électronique. Les énergies de l’orbitale occupée de plus haute énergie (HO, en anglais HOMO) et de l’orbitale vacante de plus basse énergie (BV, en anglais LUMO) sont des indices de nucléophilie et d’électrophilie, respectivement.
- Les charges « atomiques », qui de toute façon impliquent toujours une attribution plus ou moins arbitraire des électrons à chaque noyau (ne pas oublier qu’il n’y a pas, à proprement parler, d’atomes dans les molécules !). Les valeurs rapportées ici sont les « populations de Mulliken » (cf. ExemplesSCF.pdf, page 8).
Les calculs sont effectués pour une molécule isolée, c’est-à-dire dans le vide. Les énergies orbitalaires des ions
positifs sont fortement abaissées par rapport à leur valeur en solution. C’est pourquoi nous présentons également des
résultats en solution dans un solvant indiqué entre parenthèses, généralement le méthanol. Le solvant est modélisé par
un continuum polarisable.
Certains ions négatifs, en particulier dans des complexes, présentent des énergies orbitalaires positives, ce qui
signifierait la perte spontanée d’un ou plusieurs électrons. Ces résultats aberrants peuvent provenir d’une
insuffisance du niveau de calcul, de l’absence de solvant ou de contre-ions. Nous les donnons cependant sous réserve,
la structure des OM et leurs énergies relatives conservant un caractère indicatif.
Les molécules contenant des éléments non paramétrés en AM1 sont traitées au niveau Hartree-Fock avec la base STO-3G. Les complexes modèles MLn et les fragments correspondants M et Ln sont calculés par la méthode de Hückel généralisée (EHMO).
Erreurs
Depuis la mise en service du site, nous avons corrigé un certain nombre d’erreurs. Il en reste surement, n’hésitez pas à nous les signaler.
Sur les petites molécules
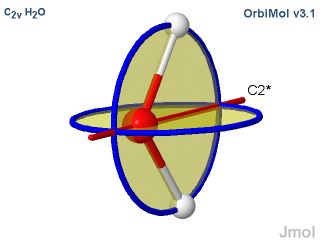
Selon les conventions de la théorie des groupes, l’axe
d’ordre supérieur est pris comme axe z. Par exemple, dans les molécules
pyramidales comme NH3 (groupe C3v) l’axe z est l’axe
d’ordre 3. Dans les molécules AX2, c’est l’axe d’ordre 2 ; dans
ce dernier cas cependant, la convention de placer la molécule dans le plan yz
n’a pas toujours été respectée.
Pour toutes les petites molécules inorganiques, en
particulier celles destinées à illustrer la méthode VSEPR, la géométrie
expérimentale a été utilisée. De légères différences peuvent se manifester selon les sources.
Les molécules possédant un axe d’ordre 3 ou plus
présentent des dégénérescences. Comme toute combinaison d’orbitales dégénérées
est aussi une orbitale du système, le programme délivre souvent des OM
présentant des mélanges px et py. Pour des raisons de
clarté pédagogique, nous avons pallié cet inconvénient en fournissant des OM ne contenant que (ou pratiquement que)
py ou py. Des oublis peuvent cependant subsister.
Molécules à couches incomplètes
Ces molécules présentent des électrons non
appariés : les radicaux (état doublet), le dioxygène, le carbène etc.
(état triplet) les fragments (voir plus loin). La méthode AM1 effectue un
calcul de type UHF (Unrestricted Hartree-Fock), « sans contrainte de
spin ». Cela signifie que les électrons de spin α
et les électrons de spin β sont laissés « libres » de ne pas occuper deux
à deux la même OM (cf. HartreeFock.pdf page 8). Il en
résulte effectivement des différences (souvent faibles) dans les OM des
électrons de chaque « paire » électronique. Les orbitales sont
données par le programme successivement : d’abord celle des spins α,
puis celles des spins β. Celles-ci ont été supprimées.
Forces orbitalaires « dynamiques »
On peut définir un type de force orbitalaire fondé sur le théorème de Koopmans. Ce théorème établit que l’énergie ei
de la ième orbitale occupée est égale à la différence entre l’énergie Hartree-Fock E° de la molécule neutre et celle
de la molécule ayant perdu un électron de cette OM, dans l’approximation des orbitales gelées,
c’est-à-dire en supposant que les OM de l’ion sont restées identiques à celle du neutre : ei = E° - E+
C’est pourquoi ei est peu différent de l’énergie d’ionisation de l’électron qui occupe cette OM.
Malgré les approximations que ce résultat suppose, il bénéficie d’une heureuse compensation d’erreurs qui le rend
relativement fiable, surtout pour les OM occupées de plus haute énergie (premières énergies d’ionisation).
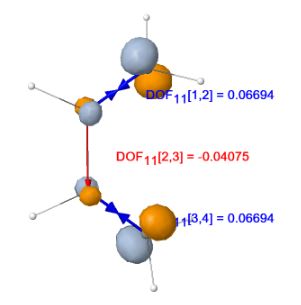
Dans le cas des molécules diatomiques de distance internucléaire R,
la dérivée de l’énergie orbitalaire par rapport à R est égale à la différence des forces s’exerçant sur les noyaux lorsqu’un
électron de cette OM a été supprimé. Si le paramètre R a été optimisé dans l’entité neutre (R = Re), la dérivée de E° par
rapport à R est nulle et on a donc égalité des dérivées par rapport à R de ei et de E+ (au signe prêt).
Après le départ de l’électron, l’énergie du système évolue en se stabilisant (relaxation), soit par l’allongement de la
liaison si e’i = dei/dR est positif, ce qui correspond au départ d’un électron liant, soit par son raccourcissement si
e’i = dei/dR est négatif (électron antiliant).
On caractérise ainsi le caractère liant/antiliant local de l’OM considérée (ici les orbitales de valence et la BV). Ces forces orbitalaires peuvent être qualifiées
de « dynamiques » (DOF, « dynamic orbital forces »), car elles n’apparaissent que lors du départ d’un électron. Pour les OM dégénérées et/ou les liaisons identiques par symétrie, la valeur moyenne de la DOF est affichée.
Fragments
La rubrique « fragments » permet notamment d’observer les orbitales
adaptées à la symétrie de groupes Hn. Pour un traitement symétrique
de tous les hydrogènes, on a placé un électron dans chacun d’entre avec des
spins parallèles (multiplicité n + 1).
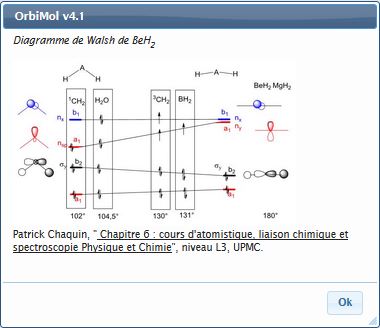
Diagrammes de Walsh
On trouvera dans cette rubrique quelques petites
molécules dans leur géométrie d’équilibre et dans une géométrie déformée
permettant d’établir des diagrammes de Walsh (cf. MoleculesAHn.pdf page
106). Ne pas oublier que la somme des énergies orbitalaires n'est pas égale à l'énergie totale dans un calcul de type Hartree-Fock.
Vibrations Moléculaires
Cette rubrique fournit les modes et les fréquences de vibration de petites molécules, calculées au niveau B3LYP
avec une base 6-311+G(dp). Les paramètres géométriques, optimisés au même niveau de calcul, peuvent différer légèrement de leur valeur expérimentale. Les modes de vibrations sont sélectionnables soit par l'animation correspondante soit par l'affichage de vecteurs. Les nombres d'onde calculés sont supérieurs d'environ 5 % à la valeur expérimentale.
Pour la création d'une vidéo, nous vous conseillons d'utiliser un programme externe comme CamStudio qui permet d'enregistrer au format AVI ce qui se passe à l'écran. L'utilisateur a le choix d'enregistrer uniquement l'activité d'une zone sélectionnée (par exemple la fenêtre Jmol) ou bien celle de la totalité de l'écran Windows.
Vous pouvez trouver ici un exemple de film.
Approche topologie de la liaison chimique
Le langage des orbitales moléculaires apporte des informations fondamentales sur une molécule et permet de préciser un certain nombre d'interactions. Toutefois, ces analyses sont fractionnées, et rendent difficile toute définition de la liaison chimique. Afin de faire apparaître les liaisons et les paires libres, il est possible d'utiliser une méthode simple et visuelle.
Fonction de Localisation Electronique :
Elle est basée sur la probabilité de trouver deux électrons de spins différents en un même point de l'espace. Plus la valeur de la fonction est élevée, plus la localisation électronique est grande. Les valeurs de la fonction ELF vont de 0 à 1. La visualisation de la fonction permet de mettre en évidence à la fois les couches électroniques de coeurs des atomes (ELF proche de 1) et aussi des domaines où la localisation électronique est intermédiaire (ELF entre 0.5 et 0.9). Les maxima de la fonction sont appelés attracteurs.
La représentation de l'isosurface (surface constituée des points ayant la même valeur de la fonction) permet de voir l'espace global de localisation. L'augmentation de la valeur de ELF définissant l'isosurface (curseur cutoff) permet de faire apparaître les différents domaines de localisation appelés bassins. Un bassin contient un seul attracteur. Ces bassins peuvent être soit partagés par plusieurs coeurs d'atomes (polysynpatiques) soit par un seul coeur (monosynaptique). Dans le premier cas, le bassin caractérise une liaison chimique et dans le deuxième cas une paire libre.
Enfin, l'intégration de la densité électronique dans les volumes définis par les différents bassins permet de calculer les populations. Par exemple, le bassin de coeur du carbone sera peuplé par 2 électrons.
Une nomenclature et un code couleur ont été établis pour faciliter cette représentation :
C(X), bassin de coeur,
V(X) bassin monosinaptique,
V(X, Y, ...) bassin polysinaptique,
V(X, H) bassin disynaptique protoné.
Prenons l'exemple de la glycine :
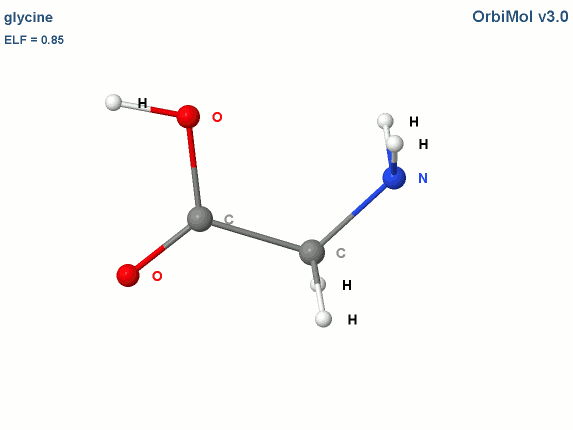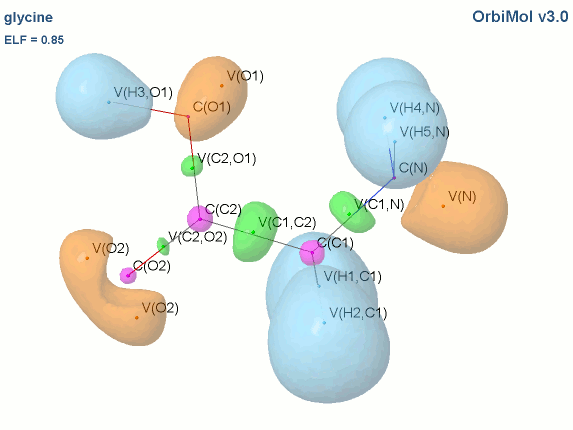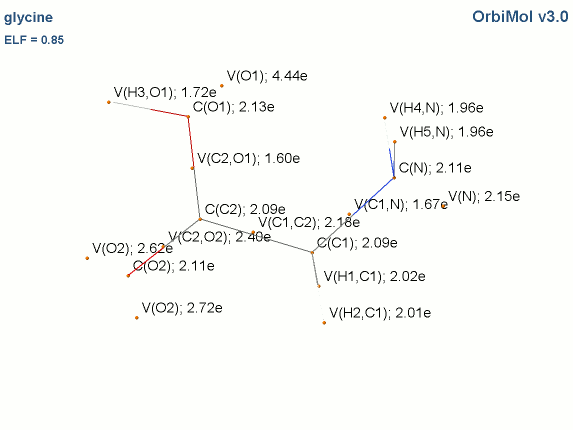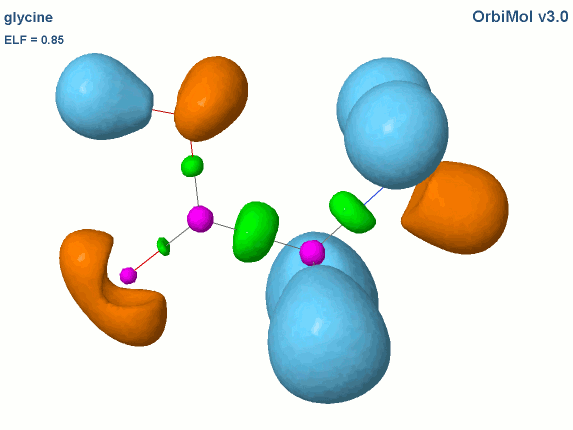
Les électrons de cœur des atomes sont représentés par des bassins magenta. Ces électrons sont fortement localisés dans ces bassins (forte valeur de l'attracteur de la fonction ELF). Comme attendu, le fichier populations indique des peuplements de 2.1 électrons pour les carbones, les oxygènes et l'azote.
Les liaisons C-C, C-O et C-N sont représentées par les bassins disynpatiques verts. Il y a bien des liaisons chimiques (covalentes) entre ces paires d'atomes. Le fichier populations indique des peuplements de 2.18 électrons pour le bassin V(C1, C2), 2.4 pour V(C2,O2) et 1.6 pour V(C2,O1), 1.67 pour V(C1,N). On peut noter que la liaison double entre C2 et O2 n'est peuplée que de 2.4 électrons contrairement au modèle de Lewis (4 électrons : 2 électrons sigma et 2 électrons pi), nous y reviendrons. Les variations observées sont dues à la délocalisation électronique au sein de la molécule et l'électronégativité des atomes composant la glycine.
Les paires libres des oxygènes et de l'azote sont représentées par les bassins monosynpatiques orange. Les populations sont de 2.15 pour V(N), de 4.44 électrons pour V(O1) et de 5.34 électrons (2.72+2.62) pour V(O2). Les deux paires libres de O2 sont surpeuplées au détriment de la population de la liaison C2-O2. L'excès est de 1.34 (5.34-4) que l'on peut attribuer au bassin V(C2,O2) ce qui lui redonne une population de 3.74 électrons (2.4+1.34). Cette valeur est proche de la population d'une liaison double au point de vue de Lewis (4 électrons).
Les hydrogènes sont représentés par des bassins bleus. Les populations sont proches de 2 électrons sauf pour le bassin V(H3,O1) qui est de 1.7 électron. La population manquante se retrouve dans le bassin V(O1) qui a un surplus de 0.44 électron (4.44-4).
Les calculs ont été réalisés en B3LYP avec une base d'orbitales 6-31+G(d). Les calculs de la fonction ELF ont été réalisés par la suite logicielle TopMod développée dans notre laboratoire.
Pour l'enseignement de la chimie, cette approche topologique fournit un support visuel de la liaison chimique.
- liaison covalente simple C2H6 : la liaison simple C-C est caractérisée par un bassin disynaptique vert et une population de 1.81e.
- liaison covalente double C2H4 : la liaison double C-C est caractérisée par deux bassins disynaptiques verts et des populations de 1.72e (un total de 3.44e). Le nombre de bassins n'est pas corrélé à la multiplicité de la liaison, mais est dû à la symétrie locale.
- liaison covalente triple C2H2 : la liaison triple C-C est caractérisée par un bassin vert torique et une population de 5.19e. La forme de ce bassin est due à la symétrie locale.
- liaison dative H3NBH3 : pour une valeur de ELF de 0.803, on peut voir que ce bassin est connecté aux hydrogènes de NH3 tandis qu'il n'est pas connecté aux hydrogènes de BH3 (connexion effective pour une valeur de ELF de 0.377). C'est pourquoi on peut affirmer que l'azote "apporte" le bassin disynaptique vert peuplé de 1.90e (paire libre de l'azote avant formation de la liaison dative).
- liaison ionique NaCl : pas de bassin vert entre les deux atomes, mais un bassin vert sur l'atome de chlore qui partage une séparatrice avec l'atome de sodium.
- liaison hydrogène (FH)2 : pas de bassin vert entre les deux FH mais ils partagent une séparatrice. Ici pas de liaison chimique mais une interaction physique.
- liaison aromatique benzène : les bassins de liaisons sont connectés (pour ELF~0.653) ce qui explique la possibilité de délocalisation électronique.
- liaison 3 centres-4 électrons (3c-4e) FHF- : liaison hydrogène forte caractérisée par deux bassins V(F, H). La somme de la population V(F,H) et V(H) est de 2.11e. Les deux électrons manquants sont situés dans les paires libres des fluores.
- liaison 3 centres-2 électrons (3c-2e) B2H6 : les deux bores sont liés à l'hydrogène peuplé par 1.91e d'où le nom de cette liaison.
- liaison 2 centres-3 électrons (2c-3e) H2S2.- : il n'y a pas de bassin disynaptique vert entre les deux soufres. La présence du troisième électron (dans une OM anitliante) induit une perte de covalence de la liaison S-S.
- H2O : on peut faire un parallèle avec la structure de Lewis de l'eau et le dessin topologique. Deux paires libres en position tétraédrique avec les deux hydrogènes. On peut enfin "voir" la place occupée par ces paires libres et expliquer facilement les répulsions au sein de cette molécule.
- H2O2 : la liaison entre les deux oxygènes est caractérisée par la présence d'un bassin disynaptique vert contenant 0.5e. On peut noter que ce bassin se sépare du reste de la valence (ELF~0.703) aussi rapidement qu'il disparaît (ELF~0.744).
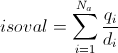où Na est le nombre d'atomes, qi est la charge de Mulliken de l'atome i et di la distance entre l'atome i et le point de la surface.
