


Next:Technique
of analysis.Up:The
topological analysis of ELFPrevious:The
topological analysis of ELF
Subsections
The
Mathematical model.
The dynamical system theory
has been pioneered at the beginning of the last century by Poincaré,
Lyapounov and Morse. It has been further developed after the fifties by
Peixoto, Arnol'd, Palis, Smale, Thom and other mathematicians. It is now
acknowledged as a general body of Mathematics.
Definitions.
Dynamical
system:
A dynamical system is
a vector field bound on a manifold 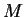 .
If this vector field is of class
.
If this vector field is of class 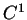 ,
the solutions of the system of equations
,
the solutions of the system of equations 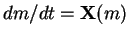 possess the property of local unicity, therefore the vector field has no
discontinuity. This system of equations interprets
possess the property of local unicity, therefore the vector field has no
discontinuity. This system of equations interprets 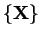 as a velocity field in which
as a velocity field in which 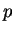 is
the time variable. This formal analogy is at the origin of the name ``dynamical
system''.
is
the time variable. This formal analogy is at the origin of the name ``dynamical
system''.

This representation of a dynamical system shows the vectors in a
plane. This kind of representation is called garden representation.
Asymptotic
behaviour:
One and only one vector
is bound to each point 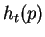 of the manifold. Therefore, the integration of
of the manifold. Therefore, the integration of 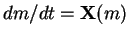 with respect to the variable
with respect to the variable 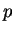 generates only one curve or trajectory. If
generates only one curve or trajectory. If 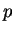 is a point belonging to
is a point belonging to 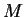 ,
the trajectory passing through
,
the trajectory passing through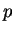 is denoted by
is denoted by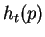 .
The limit set of
.
The limit set of 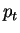 in
in 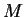 corresponding to
corresponding to 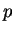 tending to
tending to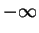 and
and 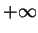 are called
are called 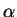 -
and
-
and 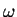 -limits,
respectively. The set of points defining the trajectories having the same
-limits,
respectively. The set of points defining the trajectories having the same 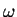 -limit
set is called stable manifold of the limit set. In the same way,
the set of points defining the trajectories having their same
-limit
set is called stable manifold of the limit set. In the same way,
the set of points defining the trajectories having their same 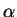 -limit
set is the unstable manifold of the
-limit
set is the unstable manifold of the 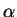 -limit
set. In a dynamical system there are two types of points: the wandering
points where
-limit
set. In a dynamical system there are two types of points: the wandering
points where 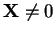 which do not belong to limit sets and the non wandering points (
which do not belong to limit sets and the non wandering points (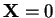 which
belong to limit sets. The set of the trajectories of a dynamical system
is called the phase portrait of this dynamical system.
which
belong to limit sets. The set of the trajectories of a dynamical system
is called the phase portrait of this dynamical system.

In this phase portrait some representative trajectories are represented.
Attractor:
An attractor is a limit
set which constitutes the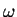 -limit
set of any points in its neighbourhood. An attractor has a stable manifold
and it does not possess an unstable manifold.
-limit
set of any points in its neighbourhood. An attractor has a stable manifold
and it does not possess an unstable manifold.
Basin
and separatrix:
The basin of an attractor 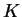 is the stable manifold of the attractor. The attractor does not belong
to its basin. The separatrix is the set of wandering points which do not
belong to a basin A separatrix is the stable manifold of a limit set which
is not an attractor.
is the stable manifold of the attractor. The attractor does not belong
to its basin. The separatrix is the set of wandering points which do not
belong to a basin A separatrix is the stable manifold of a limit set which
is not an attractor.

The two red points are the attractors of the dynamical system and the trajectories
belonging to their basins
are drawn in blue. The magenta dot is not an attractor, the green trajectories
belong to its stable manifold
and constitute the separatrix of the dynamical system.
Limit
points and characteristic exponents:
When limit sets are single
points they are characterized by their index and by their characteristic
exponents. Consider first an one dimensional dynamic system (definition
set of dimension 1). The graph of the vector field is obtained by rotating
each vector by 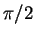 in the trigonometric sense. The Lyapounov characteristic exponent is the
slope of the curve representing the vector field at the critical point
(
in the trigonometric sense. The Lyapounov characteristic exponent is the
slope of the curve representing the vector field at the critical point
(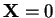 ).
).

The generalization
to 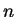 -dimensional
definition sets is straightforward and the number of critical exponents
is
-dimensional
definition sets is straightforward and the number of critical exponents
is 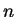 .
The index is the dimension of the unstable manifold of the critical point.
It is zero for an attractor. In the two-dimensional cases, there are two
types of limit points, the nodal and focal ones. The characteristic exponents
of a nodal limit point are real whereas those of a focal critical point
are a pair of complex conjugate numbers.
.
The index is the dimension of the unstable manifold of the critical point.
It is zero for an attractor. In the two-dimensional cases, there are two
types of limit points, the nodal and focal ones. The characteristic exponents
of a nodal limit point are real whereas those of a focal critical point
are a pair of complex conjugate numbers.
| type |
index |
characteristic
exponents (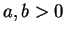 ) ) |
| focal attractor |
0 |
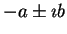 |
|
| nodal attractor |
0 |
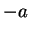 |
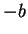 |
| saddle
point |
1 |
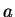 |
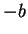 |
| focal repulsor |
2 |
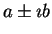 |
|
| nodal repulsor |
2 |
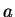 |
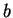 |
Three-dimensional cases
are more complicated.
| type |
index |
characteristic
exponents (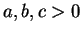 ) ) |
| focal nodal
attractor |
0 |
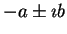 |
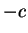 |
|
| nodal attractor |
0 |
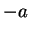 |
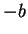 |
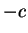 |
| focal nodal
saddle point |
1 |
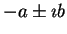 |
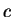 |
|
| nodal saddle
point |
1 |
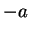 |
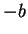 |
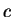 |
| focal nodal
saddle point 2 |
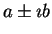 |
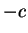 |
|
|
| nodal saddle
point |
2 |
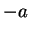 |
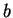 |
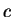 |
| focal nodal
repulsor |
3 |
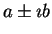 |
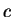 |
|
| nodal repulsor |
3 |
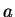 |
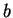 |
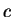 |
A limit point is hyperbolic
if all its characteristic exponents are non zero, degenerated otherwise.
Structural
stability:
The structural stability
of a dynamical system characterizes the response of the dynamical system
to a weak perturbation. A weak perturbation is a weak vector field which
is added to the dynamical system. This perturbation yields a new dynamical
system (perturbed). If the phase portraits of the perturbed and unperturbed
dynamical systems are topologically equivalent (homeomorphism), i.e. if
it is possible to go from one to the other by a continuous deformation,
the dynamical system is structurally stable.
Domain:
Consider a subset 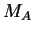 of the manifold
of the manifold 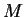 .
If two any points
.
If two any points 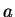 and
and 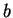 of
of 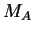 can be joined by a path totally contained in
can be joined by a path totally contained in 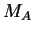 ,
,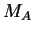 is a domain.
is a domain.
Gradient
dynamical system:
In a gradient dynamical
system, the vector field is the gradient field of a function called potential
function:
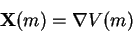
A generic property
(i.e. true except for exceptional cases) of gradient dynamical system is
that the dimension of their limit sets is 0 because the potential function
is continuous and differentiable at any point belonging to the definition
set. In 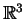 ,
these exceptions are encountered for potential functions which transforms
according to a continuous symmetry group. In the case the relevant dimension
of the space to be considered is 2 for the cylindrical symmetry, 1 for
the spherical symmetry and 0 for the group of all the translations. The
critical points all nodal points where:
,
these exceptions are encountered for potential functions which transforms
according to a continuous symmetry group. In the case the relevant dimension
of the space to be considered is 2 for the cylindrical symmetry, 1 for
the spherical symmetry and 0 for the group of all the translations. The
critical points all nodal points where:
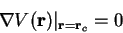
The critical exponents
are the eigenvalues of the Hessian matrix.
Number
of critical points:
The number of critical
points fulfills the Poincaré-Hopf relation:
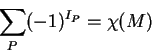
where 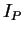 is the index of the critical point
is the index of the critical point 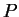 and
and 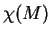 the Euler characteristic of the manifold. For aperiodic definition sets
in
the Euler characteristic of the manifold. For aperiodic definition sets
in 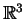 ,
,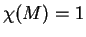 ,
for a periodic one
,
for a periodic one 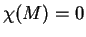 .
.
Structural
stability of gradient dynamical system:
In  a
gradient dynamical system is structurally stable if all its critical points
are hyperbolic.
a
gradient dynamical system is structurally stable if all its critical points
are hyperbolic.
Control
space:
The potential function
often depends upon of parameters 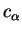 called the control parameters which are the elements of the set
called the control parameters which are the elements of the set 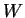 referred to as the control space of dimension k. In the case
of applications related to physics or chemistry such parameters may be
related to external constraints (i.e electric or magnetic field, external
pressure, temperature).
referred to as the control space of dimension k. In the case
of applications related to physics or chemistry such parameters may be
related to external constraints (i.e electric or magnetic field, external
pressure, temperature).
Catastrophe:
Upon the variation of
these parameters the behaviour of the the potential function changes and
therefore the phase portrait of the dynamical system may be changed. A
subset of 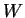 within which no change occurs is called domain of structural stability,
within a domain of structural stability the Hessian matrix is regular.
If the control space parameters are dropped from a domain of structural
stability to another the phase portrait of the dynamical system changes,
nevertheless the Poincaré-Hopf relation is always fulfilled. The
configuration of the control parameter at which the change occurs is called
a bifurcation point. At a bifurcation point the Hessian matrix of the potential
function at a given critical point is singular, therefore this point becomes
non hyperbolic and the structural stability is lost.
within which no change occurs is called domain of structural stability,
within a domain of structural stability the Hessian matrix is regular.
If the control space parameters are dropped from a domain of structural
stability to another the phase portrait of the dynamical system changes,
nevertheless the Poincaré-Hopf relation is always fulfilled. The
configuration of the control parameter at which the change occurs is called
a bifurcation point. At a bifurcation point the Hessian matrix of the potential
function at a given critical point is singular, therefore this point becomes
non hyperbolic and the structural stability is lost.



Next:Technique
of analysis.Up:The
topological analysis of ELFPrevious:The
topological analysis of ELF
bernard
2002-04-01





![]() -dimensional
definition sets is straightforward and the number of critical exponents
is
-dimensional
definition sets is straightforward and the number of critical exponents
is ![]() .
The index is the dimension of the unstable manifold of the critical point.
It is zero for an attractor. In the two-dimensional cases, there are two
types of limit points, the nodal and focal ones. The characteristic exponents
of a nodal limit point are real whereas those of a focal critical point
are a pair of complex conjugate numbers.
.
The index is the dimension of the unstable manifold of the critical point.
It is zero for an attractor. In the two-dimensional cases, there are two
types of limit points, the nodal and focal ones. The characteristic exponents
of a nodal limit point are real whereas those of a focal critical point
are a pair of complex conjugate numbers.
![]() ,
these exceptions are encountered for potential functions which transforms
according to a continuous symmetry group. In the case the relevant dimension
of the space to be considered is 2 for the cylindrical symmetry, 1 for
the spherical symmetry and 0 for the group of all the translations. The
critical points all nodal points where:
,
these exceptions are encountered for potential functions which transforms
according to a continuous symmetry group. In the case the relevant dimension
of the space to be considered is 2 for the cylindrical symmetry, 1 for
the spherical symmetry and 0 for the group of all the translations. The
critical points all nodal points where:
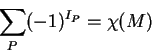
![]() is the index of the critical point
is the index of the critical point ![]() and
and ![]() the Euler characteristic of the manifold. For aperiodic definition sets
in
the Euler characteristic of the manifold. For aperiodic definition sets
in ![]() ,
,![]() ,
for a periodic one
,
for a periodic one ![]() .
.