


suivant: Principe variationnel
monter: Exemple: calcul de la
précédent: Méthode de variation des
La fonction d'onde perturbée au premier ordre est écrite sous la forme de
la somme de deux composantes:
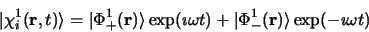 |
(3.99) |
En substituant dans 3.92, on obtient pour
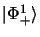 et
et
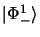
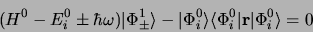 |
(3.100) |
En développant sur les fonctions propres de 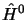 :
:
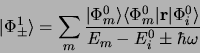 |
(3.101) |
et
![\begin{displaymath}
\alpha(\omega)=\sum\limits_m\vert\langle\Phi^{0}_m\vert {\bf...
...c{1}{E_m-E_i+\hbar\omega}+\frac{1}{E_m-E_i-\hbar\omega}\right]
\end{displaymath}](img926.png) |
(3.102) |
Bernard Silvi
2005-03-16
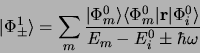
![\begin{displaymath}
\alpha(\omega)=\sum\limits_m\vert\langle\Phi^{0}_m\vert {\bf...
...c{1}{E_m-E_i+\hbar\omega}+\frac{1}{E_m-E_i-\hbar\omega}\right]
\end{displaymath}](img926.png)