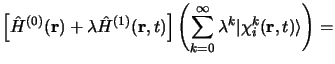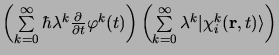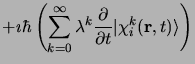suivant: Exemple: calcul de la
monter: Perturbation dépendant du temps.
précédent: Méthode de variation des
Méthode de variation perturbation.
La méthode de variation des constantes ne permet pas de retrouver les
équations de la perturbation statique, dans la limite où 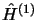 est indépendant du temps. Dans la méthode de variation perturbation,
l'équation de Schrödinger perturbée s'écrit:
est indépendant du temps. Dans la méthode de variation perturbation,
l'équation de Schrödinger perturbée s'écrit:
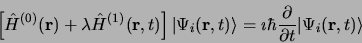 |
(3.84) |
et la fonction propre
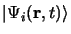 est développée en
série du paramètre de perturbation
est développée en
série du paramètre de perturbation 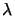 :
:
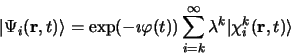 |
(3.85) |
où le facteur de phase 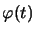 est lui-même développé en série
de
est lui-même développé en série
de 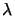
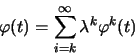 |
(3.86) |
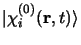 est choisi
tel qu'il soit fonction propre de l'équation de Schrödinger non perturbée:
est choisi
tel qu'il soit fonction propre de l'équation de Schrödinger non perturbée:
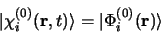 |
(3.87) |
ce qui implique
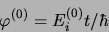 |
(3.88) |
De plus on impose à
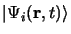 d'être normée.
En substituant 3.85 et 3.86 dans 3.84
et après avoir multiplier chaque membre par
d'être normée.
En substituant 3.85 et 3.86 dans 3.84
et après avoir multiplier chaque membre par
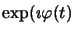 , il vient:
, il vient:
En conservant les termes de degré homogène en 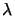 , on obtient
pour le premier ordre:
, on obtient
pour le premier ordre:
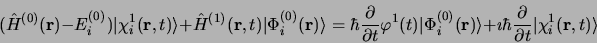 |
(3.90) |
En multipliant à gauche par
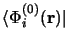 ,
on trouve :
,
on trouve :
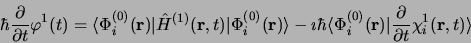 |
(3.91) |
En substituant dans 3.90 on obtient:
Si 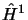 est indépendant du temps, l'équation 3.92 se
ramène à celle de la perturbation statique:
est indépendant du temps, l'équation 3.92 se
ramène à celle de la perturbation statique:
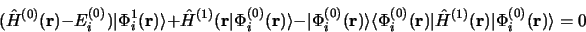 |
(3.93) |
La fonction d'onde perturbée est alors évaluée à l'aide des mêmes
techniques que dans le cas de la perturbation indépendant du temps.



suivant: Exemple: calcul de la
monter: Perturbation dépendant du temps.
précédent: Méthode de variation des
Bernard Silvi
2005-03-16