


suivant: Matrices hermitiennes.
monter: Matrices.
précédent: Combinaisons linéaires.
Si 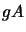 est carrée d'ordre
est carrée d'ordre 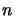 , la matrice
, la matrice
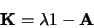 |
(1.18) |
est appelée matrice caractéristique de
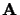 . L'équation
. L'équation
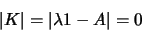 |
(1.19) |
est l'équation caractéristique de 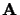 .
par
.
par
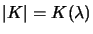 est un polynôme d'ordre
est un polynôme d'ordre 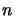 en
en
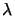 dont les racines sont les racines de la matrice
dont les racines sont les racines de la matrice 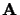 .
.
Si
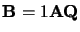 alors
alors
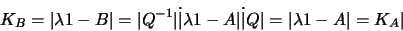 |
(1.20) |
La relation
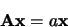 |
(1.21) |
où 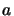 est un scalaire et
est un scalaire et 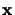 un vecteur colonne est l''equations aux
valeurs propres de
un vecteur colonne est l''equations aux
valeurs propres de 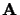 . Cette équation peut s'écrire
. Cette équation peut s'écrire
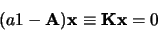 |
(1.22) |
Les valeurs propres de 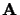 sont donc les racines de
sont donc les racines de 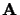 , ce qui
fournit la méthode de calcul des valeurs propres. Pour calculer les
vecteurs propres on doit résoudre les systèmes inhomogènes
, ce qui
fournit la méthode de calcul des valeurs propres. Pour calculer les
vecteurs propres on doit résoudre les systèmes inhomogènes
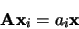 |
(1.23) |
les 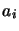 étant les valeurs propres. Il est pratique de regrouper les
vecteurs propres et les valeurs propres dans des matrices:
étant les valeurs propres. Il est pratique de regrouper les
vecteurs propres et les valeurs propres dans des matrices:
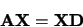 |
(1.24) |
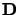 est la matrice diagonale des valeurs propres
est la matrice diagonale des valeurs propres
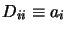
Si l'on multiplie à gauche par 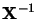 l'équation
précédant
l'équation
précédant
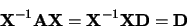 |
(1.25) |



suivant: Matrices hermitiennes.
monter: Matrices.
précédent: Combinaisons linéaires.
Bernard Silvi
2005-03-16
![]() est carrée d'ordre
est carrée d'ordre ![]() , la matrice
, la matrice
![]() alors
alors
![]() l'équation
précédant
l'équation
précédant