Towards the QM/MM modeling of complex biosystems with Density Functional Theory and other tools

Dennis R. Salahub

University of Calgary

2500 University Drive NW

Calgary, Alberta T2N 1N4

Canada

Density Functional Theory has progressed remarkably over the years, developing from fringe applications to its current state as a mainstay of computational chemistry, physics and biology. Many frontiers have been traversed: structure optimization, excited states, spectroscopies of various types, reactivity and dynamics. Much current effort is focused on hybrid methods that combine DFT with forcefields of various types in order to treat a quantum mechanical core with an adequate description of environmental effects.

One of the current “last frontiers of DFT” lies in the area of weak intermolecular interactions. Roughly speaking, good results can be obtained for hydrogen-bonded systems with contemporary functionals of the Generalized Gradient Approximation (GGA) or so-called meta-GGA functionals. Weaker non-bonded interactions, such as those found in the stacking of DNA bases, or mid-range interactions in peptides are presently not under control; GGA and meta-GGA functionals fail.

We are exploring a number of potential approaches to develop new functionals and methodologies that are appropriate for interactions in the important 3-5 Angstrom range. Van der Waals interactions in this range often have a large “dispersion” contribution (although the definition of dispersion is clouded by overlap effects).

The paper will present an overview of non-bonded interactions of the hydrogen bonding and stacking types and report progress on schemes that incorporate an empirical damped dispersion correction[1]. The damping function is optimized on a small, well balanced set of 22 van der Waals complexes and verified on a validation set of 58 vdW complexes. Both sets contain biologically relevant molecules such as nucleic acid bases. Results are in remarkable agreement with reference high-level wave function data based on the CCSD(T) method. On average, the dispersion contribution to the interaction energy missing in the DFT functionals examined here is about 15% and 100% for the hydrogen-bonded and stacked complexes considered, respectively.

Most recently, we have reparameterized a meta-GGA functional, TPSS-Tau3, using a training set that contains van der Waals systems. The results are most encouraging; it seems that the meta-GGA class of functionals can be “stretched” into the important 3-5 Angstrom region.

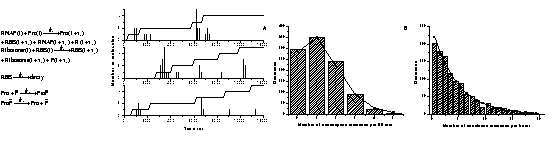
A potential future application of these techniques is in the area of genetic regulatory networks[2]. Current advances in molecular biology enable us to access rapidly increasing genetic information, and guided by models, we can understand further the gene world. It is still challenging to model gene systems at the molecular level. Here, we propose two types of reaction kinetic models for constructing genetic networks. One is based on delayed effective reactions, each modeling a biochemical process like transcription without involving intermediate reactions. The other is based on delayed virtual reactions, each being converted from a mathematical function to model a biochemical function like gene inhibition. The latter stochastic models are derived from the corresponding mean-field models. The former ones are composed of single gene expression modules. We thus design a model of gene expression. This model is verified by our simulations using a delayed Gillespie algorithm, which accurately reproduces the stochastic kinetics in a recent experimental study that followed the synthesis of a protein one molecule at a time[3]. The agreement between experiment (upper figures) and our simulations (lower figures) is striking:

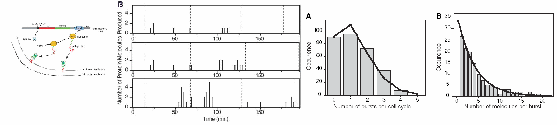
Various simplified versions of the model, including a widely used one in the literature, are given, and evaluated by comparing their kinetics. It is found that the literature model may cause significant errors in quantitative studies. We then use the two methods to study the genetic toggle switch and the repressilator. We define the “on” and “off” states of genes and extract the binary code from the stochastic time series. The binary code can be accurately described by the corresponding Boolean network models in certain conditions. We discuss these conditions, suggesting a method to connect Boolean network models, mean-field models, and stochastic chemical models in studying genetic networks.

In the fullness of time the rate constants that control genetic networks will be calculated from first principles rather than being introduced as empirical parameters. The work reported in the first part of the paper is a necessary preparative step along the way.

References

1. Petr Jurečka, Jiří Černý, Pavel Hobza , Dennis R. Salahub J. Comput. Chem in press..

2. Rui Zhu, Andre S. Ribeiro, Dennis Salahub, and Stuart A. Kauffman Genome Research submitted.

3. J.Yu, J. Xiao, X.Ren, K.Lao, S.Xie, Science 311 1600-1603 (2006).