5.3 MXVA: matrix-vector product

      subroutine mxva(a,mcola,mrowa,b,mcolb,
     1                r,mcolr,ncol,nlink)
      implicit double precision (a-h,o-z)
      dimension r(1),a(1),b(1)

calculates the 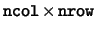${\tt ncol}\times{\tt nrow}$ matrix product $\bf r = A b$.

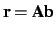a

real array containing the matrix 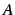$A$; note that the matrix may be supplied transposed, with non-unit stride, and with enlarged leading dimension, under the control of the parameters mcola, mrowa described below.

mcola

memory increment in a between adjacent columns of $A$.

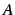mrowa

memory increment in a between adjacent rows of $A$.

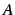b

real array containing the vector $b$

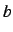
mcolb

memory increment in b between adjacent elements of $b$.

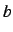r

real array containing the vector 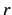$r$; r is cleared to zero at the start of mxma, and so any previous contents are lost.

mcolr

memory increment in r between adjacent elements of $r$.

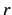ncol

number of rows in 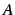$A$ and elements in $r$.

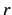nlink

dimension which is summed over: number of elements in 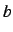$b$ and number of columns in $A$.

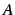Thus standard use of mxva would take the form

      call mxva(a,1,nlink,b,1,r,1,ncol,nlink)