5.1 MXMA: matrix-matrix product

      subroutine mxma(a,mcola,mrowa,b,mcolb,mrowb,
     *r,mcolr,mrowr,ncol,nlink,nrow)
      implicit double precision (a-h,o-z)
      dimension r(1),a(1),b(1)

calculates the 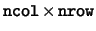${\tt ncol}\times{\tt nrow}$ matrix product $\bf R = A B$.

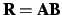a

real array containing the matrix 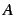$A$; note that the matrix may be supplied transposed, with non-unit stride, and with enlarged leading dimension, under the control of the parameters mcola, mrowa described below.

mcola

memory increment in a between adjacent columns of $A$.

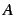mrowa

memory increment in a between adjacent rows of $A$.

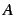b

real array containing the matrix $B$

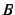
mcolb

memory increment in b between adjacent columns of $B$.

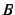mrowb

memory increment in b between adjacent rows of $B$.

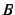r

real array containing the matrix 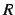$R$; r is cleared to zero at the start of mxma, and so any previous contents are lost.

mcolr

memory increment in r between adjacent columns of $R$.

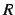mrowr

memory increment in r between adjacent rows of $R$.

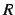ncol

number of rows in 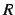$R$ and $A$.

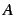nlink

dimension which is summed over: number of rows in 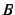$B$ and number of columns in $A$.

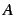nrow

number of columns in 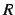$R$ and $B$.

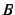Thus standard use of mxma would take the form

      call mxma(a,1,nlink,b,1,nrow,r,1,nrow,ncol,nlink,nrow)

whilst, for example,

      call mxma(a,1,nlink,b,nrow,1,r,1,nrow,ncol,nlink,nrow)

would multiply a(ncol,nlink) by the transpose of b(nrow,link).