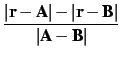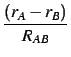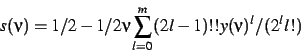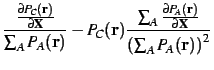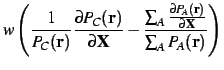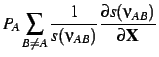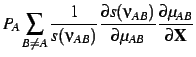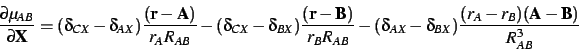Next: 11.3 Evaluation of orbitals
Up: 11.2.9 grid_obtain_gradwt: obtain a
Previous: 11.2.9 grid_obtain_gradwt: obtain a
The weight at a grid point is defined
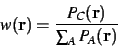 |
(7) |
where
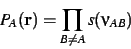 |
(8) |
in which
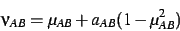 |
(9) |
Note that 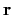 is tied to atom
is tied to atom 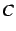 , i.e.,
, i.e.,
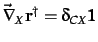 .
We define
.
We define
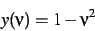 |
(12) |
and 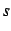 chosen such that
chosen such that
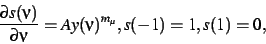 |
(13) |
i.e.,
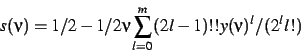 |
(14) |
We require the derivatives of the grid weights with respect to
nuclear coordinates.
So, we apply the chain rule recursively; firstly, the derivative of
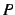 in terms of the derivatives of
in terms of the derivatives of 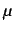 :
:
Next, differential properties of 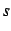 :
:
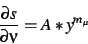 |
(19) |
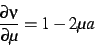 |
(20) |
Hence
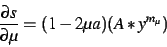 |
(21) |
Finally, derivatives of 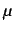 :
:
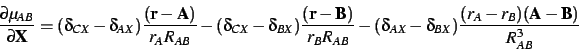 |
(22) |
Next: 11.3 Evaluation of orbitals
Up: 11.2.9 grid_obtain_gradwt: obtain a
Previous: 11.2.9 grid_obtain_gradwt: obtain a
P.J. Knowles and H.-J. Werner
molpro-support@tc.bham.ac.uk
Jan 10, 2000