Table 10:
Summary of attenuate options and their default values
| Parameter |
Default value |
Meaning |
| |
|
|
| Most important options: |
| DECAY |
0.20 |
split parameter 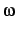 |
| SHORTMLT |
15 |
level 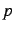 of monopolar multipole expansion of monopolar multipole expansion |
| LONGMLT |
13 |
level 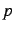 of bipolar multipole expansion of bipolar multipole expansion |
| |
|
|
| Specifying which integrals to treat
by which multipole expansion type: |
| RMAIN |
1 |
when to switch from monopolar to four-block treatment |
| RIONIC |
0 |
when to switch from monopolar to bipolar treatment of ionic blocks |
| SUPPRESS |
0 |
when to suppress cross-excited blocks |
| |
|
|
| Options for least squares fit generation of interaction coefficiets: |
| FITMLTP |
1 |
use least squares fit instead of Taylor |
| F1DGRID |
50 |
no. of quadrature points for 1D fit |
| F2DGRIDR |
50 |
no. of quadrature points for 2D fit 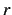 |
| F2DGRIDP |
20 |
no. of quadrature points for 2D fit 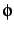 |
| F1DBORDER |
0 |
end of integration interval for 1D fit |
| F2DBORDER |
0 |
end of integration interval for 2D fit 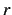 |
| F1DGAMMA |
1.7 |
negative exponent of weight function for 1D fit |
| F2DGAMMA |
1.7 |
negative exponent of weight function for 2D fit |
| WEIGHT3D |
1 |
use spacial instead of flat weight function |
| |
|
|
| Options for determination of batches: |
| NUMBATCH |
0 |
manually set number of batches |
| BATCHDIAM |
35 |
maximal diameter of batches |
| BATCHALGO |
2 |
algorithm to determine batches |
| WEIGHTPREV |
0.5 |
parameter for algorithm BATCHALGO=1 |
| RANSEED |
-1 |
initialize random number generator for simulated annealing |
| |
|
|
| Further numerical stability options: |
| CUTOFF |
15 |
orbital cutoff |
| MONOPOLE |
1 |
if and how to treat monopole integrals |
| |
|
|
| Multipole operators: |
| MAXMLTPL |
auto |
manually set level of multipole operators to create |
| MULTPAGE |
1 |
turn on paging of multipole operators during multipole expansion |
| |
|
|
| Essentially obsolete keys (for Taylor expansion): |
| TRUNCATE |
0 |
truncation pattern of multipole expansion |
| DAMP |
0 |
damping function for orbitals |
| SCALEDAMP |
0 |
scaling factor for the damping function |
| |
|
|
| Stuff for debugging: |
| PAIREN |
0 |
print a list of uncoupled pair energies |