Quadratic response

 

An example of a quadratic response  function is the first hyperpolarizability . If we are interested in the component only we may use the following input:

**DALTON INPUT
.RUN RESPONSE
**WAVE FUNCTIONS
.HF
**RESPONSE
*QUADRATIC
.DIPLNZ
*END OF INPUT

When no frequencies are given in the input, the static value is assumed by default. If we wish to calculate dynamic hyperpolarizabilities we supply frequencies , but in this case we have two frequencies which are given by the keywords .BFREQ and .CFREQ (see the Reference Manual, chapter ).

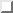The residue of a quadratic response function gives two-photon transition amplitudes . For such a calculation we supply the same extra keywords as in the linear case (Sec. ):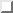

**RESPONSE
*QUADRATIC
.DIPLNZ
.SINGLE RESIDUE
.ROOTS
 2 0 0 0
*END OF INPUT

which in this case means the two-photon transition amplitude  between the reference state and the first two excited states in the first symmetry. In general the residue of a quadratic response function corresponds to the induced transition moment of an operator A due to a perturbation B. The C operator is arbitrary and is not specified. A typical example is the dipole matrix element between a singlet and triplet state that is induced by spin-orbit coupling (phosphorescence) . For this special case we have the keyword, .PHOSPHORESCENCE under *QUADRATIC, which sets A to electric dipole operators and B to spin-orbit operators.

It is possible to construct double residues   of the quadratic response function, the interpretation of which is transition moments   between two excited states. Specifying .DOUBLE in the example above thus gives the matrix elements of the z-component of the dipole moment between all excited specified in .ROOTS. Note that the diagonal contributions gives, not the expectation value in the excited state, but rather the difference relative to the reference state expectation value.