Cartesian geometry input

  

Assuming that we have given the general input as indicated above, we now want to specify the spatial arrangements of the atoms in a Cartesian coordinate system. We will also for sake of illustration assume that we have given explicitly the generators of the point group to be used in the calculation (in this case C 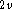, with the yz- and xz-planes as mirror planes).

In tetrahedran we will have two different kinds of atoms, carbon and hydrogen, as indicated by the number 2 on the fourth (fifth) line of the input. We will also assume that we punch the basis set ourselves, in order to present the input format for the basis set.

For tetrahedran, the input would then look like

 5:        6.    2    3    1    1    1
 6:C1    1.379495419          .0                 0.975450565  
 7:C2     .0                 1.379495419         -.975450565  
 8:    8    3
 9:486.9669   .01772582
10:73.37109   .1234779
11:16.41346   .4338754
12:4.344984   .5615042
13:8.673525            -.1213837
14:2.096619            -.2273385
15:.6046513             1.185174
16:.1835578                      1.00000
17:    4    2
18:8.673525   .06354538
19:2.096619   .2982678
20:.6046513   .7621032
21:.1835578             1.000000
22:    1    1
23:0.8        1.0
24:        1.    2    2    1    1
25:H1    3.020386510         .0                  2.1357357837 
26:H2     .0                 3.020386510         -2.1357357837
27:    4    2
28:18.73113   .03349460
29:2.825394   .2347270
30:.6401218   .8137573
31:.1612778             1.000000
32:    1    1
33:0.75       1.0

The different lines are:

5

ZMATL, CHARGE, NUMBER, MAXL, NGRP(I) (BN,A6,F4.0,24I5).

ZMATL

This field must be left blank when Cartesian coordinate input  is used as the field is used for checking whether Cartesian coordinates or Z-matrix  input is being used. Characters placed in this field will tell the program to use Z-matrix input.

CHARGE

Charge of this atom  type.

NUMBER

Number of symmetry-distinct  atoms of this type (or, if the symmetry detection routines are being used, all atoms of this kind).

MAXL

Maximum angular quantum number used in the basis set for this atom type (s=1, p=2, etc.). Not required if the basis set library is being used.

NGRP(I)

Number of groups (blocks) of generally contracted functions of angular quantum number I. The loop is over MAXL. Not required if the basis set library is used. It is noteworthy that DALTON collects all basis functions into one such shell, and evaluates all integrals arising from that shell  simultaneously, and the memory requirements grow rapidly with the number of basis functions in a shell (note for instance that four g functions actually are 36 basis functions, as there are 9 components of each g function). Memory requirements  can therefore be reduced by splitting basis functions of the quantum number into different blocks. However, this will decrease the performance of the integral  calculation.

6

NAME, X, Y, Z, FLAG (A4,3F20.15)

NAME

Atom name. A different name should be used for each atom of the same type, although this is not required.

X

x-coordinate (in atomic units, unless Ångström has been requested on line 4 of the input).

Y

y-coordinate.

Z

z-coordinate.

The Cartesian coordinates may be given in free format. However, the name of the atom must still be left four places, and no coordinates must enter the four first positions.

7

This is the other symmetry-distinct center of this type.

8

FRMT, NPRIM, NCONT, NOINT (A1,I4,2I5).

FRMT

A single character describing the input format of the basis set in this block. The default format is (8F10.4) which will be used if FRMT is left blank. In this format the first column is the orbital exponent and the seven last columns are contraction coefficients. If no numbers are given, a zero is assumed. If more than 7 contracted functions occur in a given block, the contraction coefficients may be continued on the next line, but the first column (where the orbital exponents are given) must then be left blank.

An F or f in the first position will indicate that the input is in free format. This will of course require that all contraction coefficients need to be typed in, as all numbers need to be present on each line. However, note that this options is particularly handy together with completely decontracted basis sets, as described below. Note that the program reads the free format input from an internal file that is 80 charcters long, and no line can therefore exceed 80 characters.

One may also give the format H or h. This corresponds to high precision format (4F20.8), where the first column again is reserved for the orbital exponents, and the three next lines are designated to the contraction coefficients. If no number is given, a zero is assumed. If there are more than three contracted orbitals in a given block, the contraction coefficients may be continued on the next line, though keeping the column of the orbital exponents blank.

NPRIM

Number of primitive  Gaussians in this block.

NCONT

Number of contracted  Gaussians in this block. If a zero is given, an uncontracted basis set will be assumed, and only orbital exponents need to be given.

9

EXP, (CONT(I), I=1,NCONT)

EXP

Exponent of this primitive.

CONT(I)

Coefficient of this primitive in contracted function I.

We note that the format of the orbital exponents  and the contraction  coefficients are determined from the value of FRMT defined on line 8.

10-16

These lines complete the specification of this contraction block: the s basis here.

17-21

New contraction block (see lines 8 and 9 above).

22-23

New contraction block.

24-33

Specifies a new atom type: coordinates and basis set.