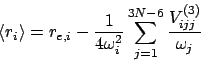 |
(16.1) |
The (ro)vibrationally averaged geometries can be calculated from a knowledge of part of the cubic force field
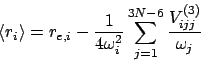 |
(16.1) |
**DALTON INPUT .WALK *WALK .ANHARM .DISPLACEMENT 0.001 .TEMPERATURES 4 0.0 300.0 500.0 1000.0 **WAVE FUNCTIONS .HF *SCF INPUT .THRESH 1.0D-10 **START *RESPONS .THRESH 1.0D-5 **EACH STEP *RESPONS .THRESH 1.0D-5 **PROPERTIES .VIBANA *RESPONS .THRESH 1.0D-5 *VIBANA .ISOTOP 3 3 1 2 1 1 2 2 2 1 1 **END OF DALTON INPUT
The calculation of (ro)vibrationally averaged geometries are invoked
be the keyword .ANHARM in the *WALK input module. In
this example, the full cubic force field will be determined as
first derivatives of analytical molecular Hessians. This will be done
in Cartesian coordinates, and the calculation will therefore require
the evaluation of ![]() analytical Hessians, where
analytical Hessians, where ![]() is the
number of atoms in the molecules. Although expensive, it allows
(ro)vibrational corrections to be calculated for any isotopic
species, in the above
example for H
is the
number of atoms in the molecules. Although expensive, it allows
(ro)vibrational corrections to be calculated for any isotopic
species, in the above
example for H![]() O, HD
O, HD![]() O, D
O, D![]() O,
H
O,
H![]() O. This is directed by the keyword
O. This is directed by the keyword .ISOTOP. We
note that the most abundant isotope will always be calculated, and is
therefore not included in the list above.
We have requested that rovibrationally averaged geometries be
calculated for 5 different temperatures. By default, these geometries
will include centrifugal distortions [16]. This can be
turned by using the keyword .NO CENT in the *WALK input
module.
By default, the numerical differentiation will use a step length of
0.0001 bohr. Experience show this to be too short [14], and we have
therefore changed this to be 0.001 bohr in the example above by the
use of the keyword .DISPLACMENT in the *WALK input
module.
If only one (or a few) isotopic species are of interest, we can significantly
speed up the calculation of the (ro)vibrationally averaged geometries
by doing the numerical differentiation in the normal coordinates of
the isotopic species of interest. This can be requested through the
keyword .NORMAL. The relevant part of the cubic force field is
then calculated as numerical second derivatives of analytical
gradients. We note that the suggested step length in this case should
be set to 0.0075 [14]. We note that we will still need to calculate one
analytical Hessian in order to determine the normal coordinates.
The default maximum number of iterations is 20. However, DALTON will
automatically reset the maximum number of iterations to 6![]() +1 in case
of vibrational averaging calculations. The maximum number of
iterations can also be set explicitly by using
the keyword
+1 in case
of vibrational averaging calculations. The maximum number of
iterations can also be set explicitly by using
the keyword .MAX IT in the **DALTON INPUT module.